题目内容
10. 如图,菱形OABC在直角坐标系中,点A的坐标为($\frac{5}{2}$,0),对角线OB=$2\sqrt{5}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)经过点C.则k的值为3.
如图,菱形OABC在直角坐标系中,点A的坐标为($\frac{5}{2}$,0),对角线OB=$2\sqrt{5}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)经过点C.则k的值为3.
分析 根据菱形的性质可知菱形的四条边都相等,点A的坐标为($\frac{5}{2}$,0),对角线OB=$2\sqrt{5}$,反比例函数y=$\frac{k}{x}$(k≠0,x>0)经过点C,可设点C的坐标为(a,b),从而可以表示出点B的坐标,然后列出相应的方程组,即可得a、b的值,从而可以得到k的值.
解答 解:∵四边形OABC是菱形,
∴OA=AB=BC=CO,
设点C的坐标为(a,b),
∵点A的坐标为($\frac{5}{2}$,0),对角线OB=$2\sqrt{5}$,
∴点B的坐标为(a+$\frac{5}{2}$,b),OC=$\frac{5}{2}$,
∴$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}=(\frac{5}{2})^{2}}\\{(a+\frac{5}{2})^{2}+{b}^{2}=(2\sqrt{5})^{2}}\end{array}\right.$,
解得a=$\frac{3}{2}$,b=2,
∴ab=$\frac{3}{2}×2=3$,
∵反比例函数y=$\frac{k}{x}$(k≠0,x>0)经过点C,点C的坐标为(a,b),
∴b=$\frac{k}{a}$,
∴k=ab=3.
故答案为:3.
点评 本题考查反比例函数图象上点的坐标特征、菱形的性质,解题的关键是根据数形结合的思想找到各边之间的关系,k与点C的坐标的关系.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
1.下列计算正确的是( )
| A. | 2a+3a=5a2 | B. | 3ab-ab=2ab | C. | 2(a2+2b)=2a2+2b | D. | 5ab-b=5a |
5. 如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.若BD=8cm,则AC的长为( )
如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.若BD=8cm,则AC的长为( )
 如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.若BD=8cm,则AC的长为( )
如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.若BD=8cm,则AC的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 6cm |
19.某同学用描点法y=ax2+bx+c的图象时,列出了表:
由于粗心,他算错了其中一个y值,则这个错误的y值是-5.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -11 | -2 | 1 | -2 | -5 | … |
20. 在一次数学实践探究活动中,大家遇到了这样的问题:
在一次数学实践探究活动中,大家遇到了这样的问题:
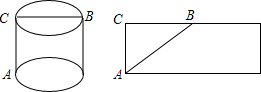
如图,在一个圆柱体形状的包装盒的底部A处有一只壁虎,在顶部B处有一只小昆虫,壁虎沿着什么路线爬行,才能以最短的路线接近小昆虫?
楠楠同学设计的方案是壁虎沿着A-C-B爬行;
浩浩同学设计的方案是将包装盒展开,在侧面展开图上连接AB,然后壁虎在包装盒的表面上沿着AB爬行.
在这两位同学的设计中,哪位同学的设计是最短路线呢?他们的理论依据是什么?( )
 在一次数学实践探究活动中,大家遇到了这样的问题:
在一次数学实践探究活动中,大家遇到了这样的问题:如图,在一个圆柱体形状的包装盒的底部A处有一只壁虎,在顶部B处有一只小昆虫,壁虎沿着什么路线爬行,才能以最短的路线接近小昆虫?
楠楠同学设计的方案是壁虎沿着A-C-B爬行;
浩浩同学设计的方案是将包装盒展开,在侧面展开图上连接AB,然后壁虎在包装盒的表面上沿着AB爬行.
在这两位同学的设计中,哪位同学的设计是最短路线呢?他们的理论依据是什么?( )
| A. | 楠楠同学正确,他的理论依据是“直线段最短” | |
| B. | 浩浩同学正确,他的理论依据是“两点确定一条直线” | |
| C. | 楠楠同学正确,他的理论依据是“垂线段最短” | |
| D. | 浩浩同学正确,他的理论依据是“两点之间,线段最短” |