题目内容
20.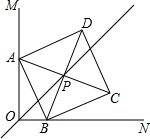 如图,∠MON=90°,线段AB的长是一个定值,点A在射线OM上,点B在射线ON上.以AB为边向右上方作正方形ABCD,对角线AC、BD交于点P,在点A从上往下,点B从左到右运动的过程中,下列说法正确的是( )
如图,∠MON=90°,线段AB的长是一个定值,点A在射线OM上,点B在射线ON上.以AB为边向右上方作正方形ABCD,对角线AC、BD交于点P,在点A从上往下,点B从左到右运动的过程中,下列说法正确的是( )| A. | 点P始终在∠MON的平分线上,且线段OP的长有最大值等于AB | |
| B. | 点P始终在∠MON的平分线上,且线段OP的长有最大值等于$\frac{\sqrt{2}}{2}$AB | |
| C. | 点P不一定在∠MON的平分线上,但线段OP的长有最小值等于AB | |
| D. | 点P不一定在∠MON的角平分线上,但线段OP的长有最小值等于$\frac{\sqrt{2}}{2}$AB |
分析 作PE⊥ON、PF⊥OM,证得△PBE≌△PAF,得出PE=PF,得出结论.
解答 解:作PE⊥ON、PF⊥OM垂足分别为E、F,
∠PEB=∠PFA=90°,
∵ABCD是正方形,
∴PA=PB,
∵∠BOA=∠BAC=90°,
∴∠DAM=∠OBA,∠POD=∠PBA=45°,
∴∠DMA+∠POD=∠PBA+∠OBA,
即∠PBE=∠PAF,
∴△PBE≌△PAF,
∴PE=PF,
即P在∠MON的平分线上,
当PE=PA时,AB=OP,
故选A.
点评 此题考查正方形的性质,关键是根据三角形全等的判定与性质,角平分线的性质分析.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.若关于x一元二次方程x2-10x+k+1=0有两个相等的实数根,则k的值为( )
| A. | 8 | B. | 9 | C. | 12 | D. | 24 |
 如图,△ABC中,∠ABC=68°,将△ABC绕点B逆时针旋转到△A′BC′的位置,使得AA′∥BC,则∠CBC′=48°.
如图,△ABC中,∠ABC=68°,将△ABC绕点B逆时针旋转到△A′BC′的位置,使得AA′∥BC,则∠CBC′=48°. 如图是正方体的一种展开图,其中每个面上都有一个数字,那么在原正方体中,与数字6相对面上的数字是( )
如图是正方体的一种展开图,其中每个面上都有一个数字,那么在原正方体中,与数字6相对面上的数字是( ) 如图,在△ABC中,点D是BC上的点,∠DAC=∠ADE,AC交DF于点F,且AC=DE.
如图,在△ABC中,点D是BC上的点,∠DAC=∠ADE,AC交DF于点F,且AC=DE.
 如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.若CD=2,则BD的长为2$\sqrt{2}$-2.
如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD.若CD=2,则BD的长为2$\sqrt{2}$-2.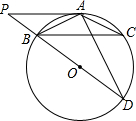 如图,⊙O是△ABC 的外接圆,AB=AC,BD是⊙O的直径,PA∥BC,与DB的延长线交于点P,连接AD.
如图,⊙O是△ABC 的外接圆,AB=AC,BD是⊙O的直径,PA∥BC,与DB的延长线交于点P,连接AD.