题目内容
8.如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=$\frac{1}{3}$,tan∠BA3C=$\frac{1}{7}$,计算tan∠BA4C=$\frac{1}{13}$,…按此规律,写出tan∠BAnC=$\frac{1}{{n}^{2}-n+1}$(用含n的代数式表示).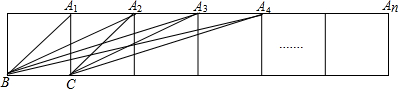
分析 作CH⊥BA4于H,根据正方形的性质、勾股定理以及三角形的面积公式求出CH、A4H,根据正切的概念求出tan∠BA4C,总结规律解答.
解答 解: 作CH⊥BA4于H,
作CH⊥BA4于H,
由勾股定理得,BA4=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$,A4C=$\sqrt{10}$,
△BA4C的面积=4-2-$\frac{3}{2}$=$\frac{1}{2}$,
∴$\frac{1}{2}$×$\sqrt{17}$×CH=$\frac{1}{2}$,
解得,CH=$\frac{\sqrt{17}}{17}$,
则A4H=$\sqrt{{A}_{4}{C}^{2}-C{H}^{2}}$=$\frac{13\sqrt{17}}{17}$,
∴tan∠BA4C=$\frac{CH}{{A}_{4}H}$=$\frac{1}{13}$,
1=12-1+1,
3=22-2+1,
7=32-3+1,
∴tan∠BAnC=$\frac{1}{{n}^{2}-n+1}$,
故答案为:$\frac{1}{13}$;$\frac{1}{{n}^{2}-n+1}$.
点评 本题考查的是正方形的性质、勾股定理的应用以及正切的概念,掌握正方形的性质、熟记锐角三角函数的概念是解题的关键.

练习册系列答案
相关题目
20.甲、乙两人用如图所示的两个转盘(每个转盘被分成面积相等的3个扇形)做游戏.游戏规则:转动两个转盘各一次,当转盘停止后,指针所在区域的数字之和为偶数时甲获胜;数字之和为奇数时乙获胜.若指针落在分界线上,则需要重新转动转盘.甲获胜的概率是( )


| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
18.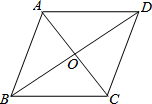 如图,菱形ABCD的对角线AC,BD的长分别为6cm,8cm,则这个菱形的周长为( )
如图,菱形ABCD的对角线AC,BD的长分别为6cm,8cm,则这个菱形的周长为( )
 如图,菱形ABCD的对角线AC,BD的长分别为6cm,8cm,则这个菱形的周长为( )
如图,菱形ABCD的对角线AC,BD的长分别为6cm,8cm,则这个菱形的周长为( )| A. | 5cm | B. | 10cm | C. | 14cm | D. | 20cm |
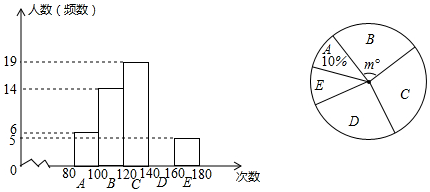

 国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.
国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.