题目内容
16.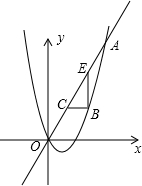 如图,已知抛物线y=$\frac{1}{2}$x2-x与直线y=2x交于O(0,0),A(a,12),点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E,以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.
如图,已知抛物线y=$\frac{1}{2}$x2-x与直线y=2x交于O(0,0),A(a,12),点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E,以BC,BE为边构造矩形BCDE,设点D的坐标为(m,n),求出m,n之间的关系式.
分析 将点A的坐标代入直线解析式求出a的值,继而将点A的坐标代入抛物线解析式可得出b的值,继而得出抛物线解析式;根据点D的坐标,可得出点E的坐标,点C的坐标,继而确定点B的坐标,将点B的坐标代入抛物线解析式可求出m,n之间的关系式.
解答 解:(1)∵点A(a,12)在直线y=2x上,
∴12=2a,
解得:a=6,
又∵点A是抛物线y=$\frac{1}{2}$x2+bx上的一点,
将点A(6,12)代入y=$\frac{1}{2}$x2+bx,可得b=-1,
∴抛物线解析式为y=$\frac{1}{2}$x2-x.
(2)∵直线OA的解析式为:y=2x,
点D的坐标为(m,n),
∴点E的坐标为($\frac{1}{2}$n,n),点C的坐标为(m,2m),
∴点B的坐标为($\frac{1}{2}$n,2m),
把点B($\frac{1}{2}$n,2m)代入y=$\frac{1}{2}$x2-x,可得m=$\frac{1}{16}$n2-$\frac{1}{4}$n,
∴m、n之间的关系式为m=$\frac{1}{16}$n2-$\frac{1}{4}$n.
点评 本题考查了矩形的性质、待定系数法求二次函数解析式的知识,解答本题需要同学们能理解矩形四个顶点的坐标之间的关系.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
 如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=152°,求∠A的度数.
如图,△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=152°,求∠A的度数.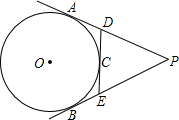 如图,PA、PB分别切⊙O于A、B两点,过劣弧$\widehat{AB}$上的一点C作⊙O的切线分别交PA、PB于D、E.求证:∠DOE=90°-$\frac{1}{2}$∠P.
如图,PA、PB分别切⊙O于A、B两点,过劣弧$\widehat{AB}$上的一点C作⊙O的切线分别交PA、PB于D、E.求证:∠DOE=90°-$\frac{1}{2}$∠P. 如图,在平面直角坐标系中,长方形OABC的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
如图,在平面直角坐标系中,长方形OABC的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E. 上海世博会区间,某博物馆每周都吸引大量中外游客前来参观,如果游客过多,对馆中的珍贵文物会产生不利影响,但同时考虑到文物的修缮和保存费用问题,还要保证一定的门票收入.因此,博物馆采取了涨浮门票价格的方法来控制参观人数,在该方法实施过程中发现:每周参观人数与票价之间存在着如图所示的一次函数关系,在这样的情况下.
上海世博会区间,某博物馆每周都吸引大量中外游客前来参观,如果游客过多,对馆中的珍贵文物会产生不利影响,但同时考虑到文物的修缮和保存费用问题,还要保证一定的门票收入.因此,博物馆采取了涨浮门票价格的方法来控制参观人数,在该方法实施过程中发现:每周参观人数与票价之间存在着如图所示的一次函数关系,在这样的情况下.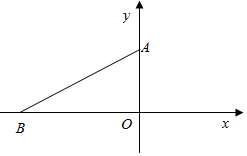 如图,已知Rt△OAB,∠OAB=60°,∠AOB=90°,O点与坐标系原点重合,若点P在x轴上,且△APB是等腰三角形,则点P的坐标可能有( )个.
如图,已知Rt△OAB,∠OAB=60°,∠AOB=90°,O点与坐标系原点重合,若点P在x轴上,且△APB是等腰三角形,则点P的坐标可能有( )个.