题目内容
9.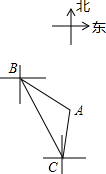 如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )| A. | 20海里 | B. | 40海里 | C. | $\frac{20\sqrt{3}}{3}$海里 | D. | $\frac{40\sqrt{3}}{3}$海里 |
分析 作AM⊥BC于M.由题意得,∠DBC=20°,∠DBA=50°,BC=60×$\frac{40}{60}$=40海里,∠NCA=10°,则∠ABC=∠ABD-∠CBD=30°.由BD∥CN,得出∠BCN=∠DBC=20°,那么∠ACB=∠ACN+∠BCN=30°=∠ABC,根据等角对等边得出AB=AC,由等腰三角形三线合一的性质得到CM=$\frac{1}{2}$BC=20海里.然后在直角△ACM中,利用余弦函数的定义得出AC=$\frac{CM}{cos∠ACM}$,代入数据计算即可.
解答 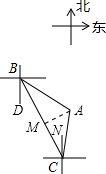 解:如图,作AM⊥BC于M.
解:如图,作AM⊥BC于M.
由题意得,∠DBC=20°,∠DBA=50°,BC=60×$\frac{40}{60}$=40海里,∠NCA=10°,
则∠ABC=∠ABD-∠CBD=50°-20°=30°.
∵BD∥CN,
∴∠BCN=∠DBC=20°,
∴∠ACB=∠ACN+∠BCN=10°+20°=30°,
∴∠ACB=∠ABC=30°,
∴AB=AC,
∵AM⊥BC于M,
∴CM=$\frac{1}{2}$BC=20海里.
在直角△ACM中,∵∠AMC=90°,∠ACM=30°,
∴AC=$\frac{CM}{cos∠ACM}$=$\frac{20}{\frac{\sqrt{3}}{2}}$=$\frac{40\sqrt{3}}{3}$(海里).
故选D.
点评 本题考查了解直角三角形的应用-方向角问题,平行线的性质,等腰三角形的判定与性质,余弦函数的定义,难度适中.求出CM=$\frac{1}{2}$BC=20海里是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列四个几何体:
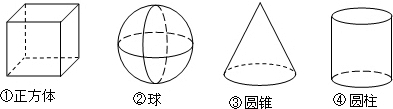
其中左视图与俯视图相同的几何体共有( )

其中左视图与俯视图相同的几何体共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.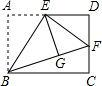 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4$\sqrt{6}$,则FD的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4$\sqrt{6}$,则FD的长为( )
 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4$\sqrt{6}$,则FD的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4$\sqrt{6}$,则FD的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{6}$ | D. | 2$\sqrt{3}$ |
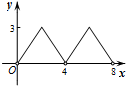
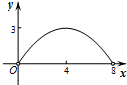
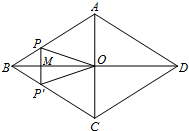 如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )
如图,菱形ABCD的对角线AC,BD相交于点O,AC=6,BD=8,动点P从点B出发,沿着B-A-D在菱形ABCD的边上运动,运动到点D停止,点P′是点P关于BD的对称点,PP′交BD于点M,若BM=x,△OPP′的面积为y,则y与x之间的函数图象大致为( )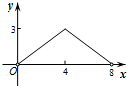
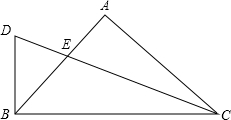 如图,在△ABC中,AB=AC,∠A=90°,CE平分∠ACB,交AB于点E,延长CE作DB⊥BC,垂足为B,则$\frac{CE}{ED}$=$\sqrt{2}$+1.
如图,在△ABC中,AB=AC,∠A=90°,CE平分∠ACB,交AB于点E,延长CE作DB⊥BC,垂足为B,则$\frac{CE}{ED}$=$\sqrt{2}$+1.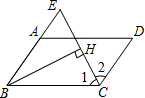 在?ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,求证:CH=EH.
在?ABCD中,∠BCD的平分线与BA的延长线相交于点E,BH⊥EC于点H,求证:CH=EH.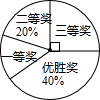 国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题: