题目内容
14.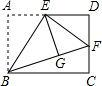 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4$\sqrt{6}$,则FD的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4$\sqrt{6}$,则FD的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{6}$ | D. | 2$\sqrt{3}$ |
分析 根据点E是AD的中点以及翻折的性质可以求出AE=DE=EG,然后利用“HL”证明△EDF和△EGF全等,根据全等三角形对应边相等可证得DF=GF;设FD=x,表示出FC、BF,然后在Rt△BCF中,利用勾股定理列式进行计算即可得解.
解答 解:∵E是AD的中点,
∴AE=DE,
∵△ABE沿BE折叠后得到△GBE,
∴AE=EG,AB=BG,
∴ED=EG,
∵在矩形ABCD中,
∴∠A=∠D=90°,
∴∠EGF=90°,
∵在Rt△EDF和Rt△EGF中,
$\left\{\begin{array}{l}{ED=EG}\\{EF=EF}\end{array}\right.$,
∴Rt△EDF≌Rt△EGF(HL),
∴DF=FG,
设DF=x,则BF=6+x,CF=6-x,
在Rt△BCF中,(4$\sqrt{6}$)2+(6-x)2=(6+x)2,
解得x=4.
故选:B.
点评 本题考查了矩形的性质,全等三角形的判定与性质,勾股定理的应用,翻折的性质,熟记性质,找出三角形全等的条件ED=EG是解题的关键.

练习册系列答案
相关题目
9.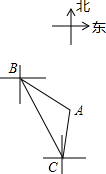 如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
 如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )
如图,轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行,在B处观测灯塔A位于南偏东50°方向上,轮船航行40分钟到达C处,在C处观测灯塔A位于北偏东10°方向上,则C处与灯塔A的距离是( )| A. | 20海里 | B. | 40海里 | C. | $\frac{20\sqrt{3}}{3}$海里 | D. | $\frac{40\sqrt{3}}{3}$海里 |
19.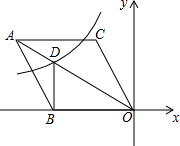 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3$\sqrt{3}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3$\sqrt{3}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3$\sqrt{3}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3$\sqrt{3}$),反比例函数y=$\frac{k}{x}$的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )| A. | 6$\sqrt{3}$ | B. | -6$\sqrt{3}$ | C. | 12$\sqrt{3}$ | D. | -12$\sqrt{3}$ |
3.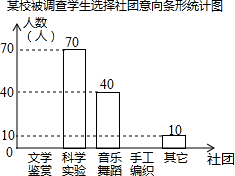 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
根据统计图表中的信息,解答下列问题:
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数.
 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):| 选择意向 | 所占百分比 |
| 文学鉴赏 | a |
| 科学实验 | 35% |
| 音乐舞蹈 | b |
| 手工编织 | 10% |
| 其他 | c |
(1)求本次调查的学生总人数及a,b,c的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数.
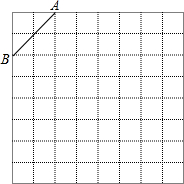 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作: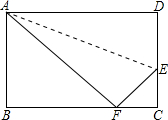 如图,在矩形ABCD中,AB=6cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,且△ABF的面积是24cm2.则AD=10cm,CE=$\frac{8}{3}$cm.
如图,在矩形ABCD中,AB=6cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,且△ABF的面积是24cm2.则AD=10cm,CE=$\frac{8}{3}$cm.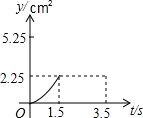
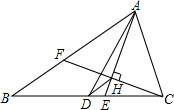 如图,在△ABC中,AB=5,AC=3,AD、AE分别为△ABC的中线和角平分线,过点C作CH⊥AE于点H,并延长交AB于点F,连结DH,则线段DH的长为1.
如图,在△ABC中,AB=5,AC=3,AD、AE分别为△ABC的中线和角平分线,过点C作CH⊥AE于点H,并延长交AB于点F,连结DH,则线段DH的长为1.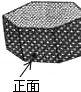 如图是某工厂要设计生产的正六棱柱形密封罐的立体图形,它的主视图是( )
如图是某工厂要设计生产的正六棱柱形密封罐的立体图形,它的主视图是( )