题目内容
17.长为1,2,3,4,5的五根木条,选其中3根组成三角形,选法有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 要把五条线段的所有组合列出来,再根据三角形的三边关系判断能组成三角形的组数.
解答 解:五根木条的所有组合:1,2,3;1,2,4;1,2,5;1,3,4;1,3,5;1,4,5;2,3,4和2,4,5和3,4,5和2,3,5;
根据三角形的三边关系,得能组成三角形的有2,3,4和2,4,5和3,4,5.
故选:C.
点评 本题考查了三角形的三边关系,熟记三角形的任意两边之和大于第三边,两边之差小于第三边是解题的关键.

练习册系列答案
相关题目
7.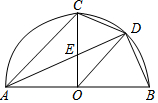 如图AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连结CD、OD,给出以下5个结论:
如图AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连结CD、OD,给出以下5个结论:
①OD∥AC;
②AC=2CD;
③2CD2=CE•AB;
④S△AEC=2S△DEO;
⑤线段OD是DE与DA的比例中项.
其中正确结论的序号( )
 如图AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连结CD、OD,给出以下5个结论:
如图AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连结CD、OD,给出以下5个结论:①OD∥AC;
②AC=2CD;
③2CD2=CE•AB;
④S△AEC=2S△DEO;
⑤线段OD是DE与DA的比例中项.
其中正确结论的序号( )
| A. | ①②③ | B. | ①④⑤ | C. | ①③④ | D. | ①③④⑤ |
8.已知代数式2x2-3x-9的值为9,则x2-$\frac{3}{2}$x-9的值为( )
| A. | $-\frac{9}{2}$ | B. | $\frac{9}{2}$ | C. | 0 | D. | -9 |
5.近似数2.70所表示的准确数a的取值范是( )
| A. | 2.695≤a<2.705 | B. | 2.65≤a<2.75 | C. | 2.695<a≤2.705 | D. | 2.65<a≤2.75 |
12.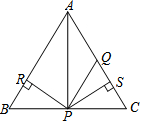 如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )
如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )
 如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )
如图,等腰△ABC中,AB=AC,AQ=PQ,PR=PS,PR⊥AB于点R,PS⊥AC于点S,则下列结论:①S△ABP=S△ACP;②AS=AR;③QP∥AB;④△BPR≌△QPS;⑤AQ=CQ中正确的有( )| A. | ①②③④ | B. | ②③④ | C. | ①③④⑤ | D. | ①②③⑤ |
2.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=-|a1+1|,a3=-|a2+2|,a4=-|a3+3|,…,依此类推,则a100的值为( )
| A. | -49 | B. | -50 | C. | -99 | D. | -100 |
9.满足下列长度的三根木棒中,能钉成一个三角形的是( )
| A. | 32,42,52 | B. | 1,$\sqrt{2}$,$\sqrt{3}$ | C. | 1,2,3 | D. | 12,22,32 |
6. 将一直角三角板与两边平行的硬纸条如图所示放置,下列结论:
将一直角三角板与两边平行的硬纸条如图所示放置,下列结论:
(1)∠1=∠2;(2)∠2+∠4=90°;(3)∠2+∠3=90°;(4)∠4+∠5=180°;(5)∠1+∠3=90°.其中正确的个数是( )
 将一直角三角板与两边平行的硬纸条如图所示放置,下列结论:
将一直角三角板与两边平行的硬纸条如图所示放置,下列结论:(1)∠1=∠2;(2)∠2+∠4=90°;(3)∠2+∠3=90°;(4)∠4+∠5=180°;(5)∠1+∠3=90°.其中正确的个数是( )
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
7.若4x2+mxy+16y2是一个完全平方式,则m的值为( )
| A. | 8 | B. | 16 | C. | ±16 | D. | ±8 |