题目内容
10.已知实数a,b满足a2-2a-1=0,b2-2b-1=0,试求$\frac{b}{a}$+$\frac{a}{b}$的值.分析 把a,b看作方程x2-2x-1=0的两个根,而$\frac{b}{a}$+$\frac{a}{b}$=$\frac{(a+b)^{2}-2ab}{ab}$,然后分类讨论并利用根与系数的关系就可以求出代数式的值.
解答 解:因为实数a,b满足等式a2-2a-1=0,b2-2b-1=0,
(1)当a=b时,原式=1+1=2;
(2)当a≠b时,可以把a,b看作是方程x2-2x-1=0的两个根.
由根与系数的关系,得a+b=2,ab=-1.
则原式=$\frac{(a+b)^{2}-2ab}{ab}$=-6.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.注意分类讨论思想的渗透.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
10.若|a-2|+|b+3|=0,则a-b-1的值为( )
| A. | 4 | B. | -6 | C. | 5 | D. | -7 |
 如图,将△ABC的一角向内折叠,使点C落在△ABC内,已知∠1=30°,∠C=40°,求∠2的度数.
如图,将△ABC的一角向内折叠,使点C落在△ABC内,已知∠1=30°,∠C=40°,求∠2的度数.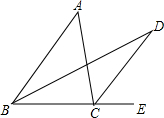 如图所示,BD,CD分比为△ABC的内角和外角的平分线,且交于点D,若∠A=50°,求∠BDC的度数,你发现了什么规律?
如图所示,BD,CD分比为△ABC的内角和外角的平分线,且交于点D,若∠A=50°,求∠BDC的度数,你发现了什么规律?