题目内容
3.计算:$\frac{1}{1×3}$+$\frac{1}{2×4}$+$\frac{1}{3×5}$+…+$\frac{1}{9×11}$.分析 先把各个分数拆分成两个分数差的形式,再抵消后即可求解.
解答 解:$\frac{1}{1×3}$+$\frac{1}{2×4}$+$\frac{1}{3×5}$+…+$\frac{1}{9×11}$
=$\frac{1}{2}$×(1-$\frac{1}{3}$+$\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{9}$-$\frac{1}{11}$)
=$\frac{1}{2}$×(1+$\frac{1}{2}$-$\frac{1}{10}$-$\frac{1}{11}$)
=$\frac{1}{2}$×$\frac{72}{55}$
=$\frac{36}{55}$.
点评 考查了有理数的混合运算,关键是熟悉$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$)的知识点.

练习册系列答案
相关题目
12.$\sqrt{{a}^{2}}$等于( )
| A. | a | B. | -a | C. | ±a | D. | 以上都不对 |
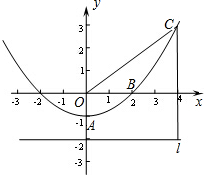 如图,已知抛物线y=ax2+c经过A(0,-1)和B(2,0),在x轴下方有一直线l,它的解析式是y=-2(即l上每点的纵坐标都是-2).
如图,已知抛物线y=ax2+c经过A(0,-1)和B(2,0),在x轴下方有一直线l,它的解析式是y=-2(即l上每点的纵坐标都是-2).