题目内容
4.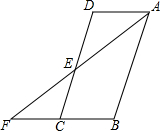 如图,在?ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.
如图,在?ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
分析 (1)利用平行四边形的性质得出AD∥BC,AD=BC,证出∠D=∠ECF,由ASA即可证出△ADE≌△FCE;
(2)证出AB=FB,由等腰三角形的性质和三角形内角和定理即可得出答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴∠D=∠ECF,
在△ADE和△FCE中,$\left\{\begin{array}{l}{∠D=∠ECF}&{\;}\\{DE=CE}&{\;}\\{∠AED=∠FEC}&{\;}\end{array}\right.$,
∴△ADE≌△FCE(ASA);
(2)解:∵△ADE≌△FCE,
∴AD=FC,
∵AD=BC,AB=2BC,
∴AB=FB,
∴∠BAF=∠F=36°,
∴∠B=180°-2×36°=108°.
点评 此题主要考查了平行四边形的性质,全等三角形的判定与性质,等腰三角形的性质、三角形内角和定理;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键..

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
14.下列命题是真命题的是( )
| A. | 菱形的对角线互相平分 | |
| B. | 一组对边平行,一组对边相等的四边形是平行四边形 | |
| C. | 对角线互相垂直且相等的四边形是正方形 | |
| D. | 对角线相等的四边形是矩形 |
19.要使式子$\frac{{\sqrt{x+2}}}{x-1}$有意义,则x的取值范围是( )
| A. | x≥-2 | B. | x≤-2 | C. | x≥1 | D. | x≥-2 且x≠1 |
13.纽约、悉尼与北京的时差如下表(正数表示同一时刻比北京时间早的时数,负数表示同一时刻比北京时间晚的时数):
当北京6月15日23时,悉尼、纽约的时间分别是( )
| 城市 | 悉尼 | 纽约 |
| 时差/时 | +2 | -13 |
| A. | 6月16日1时;6月15日10时 | B. | 6月16日1时;6月14日10时 | ||
| C. | 6月15日21时;6月15日10时 | D. | 6月15日21时;6月16日12时 |
 如图是抛物线y=ax2+bx+c(a≠0),其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,下列结论:
如图是抛物线y=ax2+bx+c(a≠0),其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间,下列结论: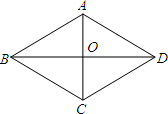 求证:对角线互相垂直的平行四边形是菱形.
求证:对角线互相垂直的平行四边形是菱形.