题目内容
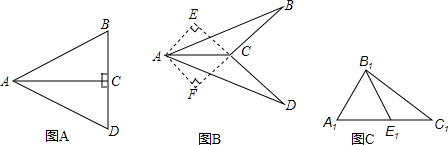
同学们知道:只有两边和其中一边的对角对应相等的两个三角形不一定全等.在△ABC中和△ADC中,AB=AD,∠BCA=∠DCA,当∠BCA分别为“直角、钝角、锐角”时,探究这两个三角形会不会全等.
(1)填空:如图A,当∠BCA是直角时:
∵△ABC和△ADC,AB=AD,AC=AC,∠BCA=∠DCA=90°.
∴△ABC≌△ADC .(从SAS、ASA、AAS、SSS、HL中选取一项作为理由)
(2)如图B,当∠BCA是钝角时,求证:△ABC≌△ADC.(提示:过点A作AE⊥DC交DC的延长线于E,过点作AF⊥BC交BC的延长线于F)
(3)当∠BCA是锐角时,△ABC和∠ADC不一定全等.
例如:如图C,在△A1B1C1和△E1B1C1中,A1B1=B1E1,∠B1C1A1=∠B1C1E1,B1C1=B1C1,但是这两个三角形不全等.
当∠BCA满足什么条件时,可得△ABC≌△ADC?请直接写出这个条件: .
(1)填空:如图A,当∠BCA是直角时:
∵△ABC和△ADC,AB=AD,AC=AC,∠BCA=∠DCA=90°.
∴△ABC≌△ADC
(2)如图B,当∠BCA是钝角时,求证:△ABC≌△ADC.(提示:过点A作AE⊥DC交DC的延长线于E,过点作AF⊥BC交BC的延长线于F)
(3)当∠BCA是锐角时,△ABC和∠ADC不一定全等.
例如:如图C,在△A1B1C1和△E1B1C1中,A1B1=B1E1,∠B1C1A1=∠B1C1E1,B1C1=B1C1,但是这两个三角形不全等.
当∠BCA满足什么条件时,可得△ABC≌△ADC?请直接写出这个条件:

考点:全等三角形的判定与性质
专题:
分析:(1)直角三角形中,根据一条直角边和斜边判定三角形全等方法为“HL”方法;
(2)易证∠ACE=∠ACF,即可证明△AEC≌△AFC,可得AE=AF,即可证明RT△ADE≌RT△ABF,可得∠B=∠D,即可证明△ABC≌△ADC,(AAS);
(3)如图所示,∠BAE是锐角,而∠BEC是钝角,AB=BE,此时添加条件∠BCA≥∠BAC,则可使得∠BAE只能是锐角,即可解题.
(2)易证∠ACE=∠ACF,即可证明△AEC≌△AFC,可得AE=AF,即可证明RT△ADE≌RT△ABF,可得∠B=∠D,即可证明△ABC≌△ADC,(AAS);
(3)如图所示,∠BAE是锐角,而∠BEC是钝角,AB=BE,此时添加条件∠BCA≥∠BAC,则可使得∠BAE只能是锐角,即可解题.
解答:解:(1)HL;
(2)过点A作AE⊥DC交DC的延长线于E,过点作AF⊥BC交BC的延长线于F,
∵∠BCA=∠DCA,
∴∠ACE=∠ACF,
在△AEC和△AFC中,
,
∴△AEC≌△AFC,(AAS)
∴AE=AF,
在RT△ADE和RT△ABF中,
,
∴RT△ADE≌RT△ABF(HL),
∴∠B=∠D,
在△ABC和△ADC中,
,
∴△ABC≌△ADC(AAS);
(3)∠BCA≥∠BAC,
理由:在△A1B1C1和△E1B1C1中,A1B1=B1E1,∠B1C1A1=∠B1C1E1,B1C1=B1C1,但是这两个三角形不全等.
不全等原因是因为∠BAE可以是锐角也可以是钝角,
添加条件∠BCA≥∠BAC,此时∠BAC只能是锐角,
故此时用“SAS”方法即可判定△ABC≌△ADC.
(2)过点A作AE⊥DC交DC的延长线于E,过点作AF⊥BC交BC的延长线于F,
∵∠BCA=∠DCA,
∴∠ACE=∠ACF,
在△AEC和△AFC中,
|
∴△AEC≌△AFC,(AAS)
∴AE=AF,
在RT△ADE和RT△ABF中,
|
∴RT△ADE≌RT△ABF(HL),
∴∠B=∠D,
在△ABC和△ADC中,
|
∴△ABC≌△ADC(AAS);
(3)∠BCA≥∠BAC,
理由:在△A1B1C1和△E1B1C1中,A1B1=B1E1,∠B1C1A1=∠B1C1E1,B1C1=B1C1,但是这两个三角形不全等.
不全等原因是因为∠BAE可以是锐角也可以是钝角,
添加条件∠BCA≥∠BAC,此时∠BAC只能是锐角,
故此时用“SAS”方法即可判定△ABC≌△ADC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△AEC≌△AFC和RT△ADE≌RT△ABF是解题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
下列方程中是一元一次方程的有( )
| A、x+3=y+2 | ||
| B、1-3(1-2x)=-2(5-3x) | ||
C、x-1=
| ||
D、
|
把抛物线y=x2+bx+c向右平移3个单位,再向下平移2个单位,得到抛物线y=x2-3x+5,则有( )
| A、b=3,c=7 |
| B、b=-9,c=-15 |
| C、b=3,c=3 |
| D、b=-9,c=21 |
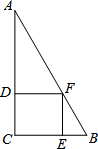 如图,已知在Rt△ABC中,∠C=90°,正方形DCEF的顶点D、E、F分别在边AC、BC、AB上,如果AC=10,BC=6,那么正方形DCEF的边长为
如图,已知在Rt△ABC中,∠C=90°,正方形DCEF的顶点D、E、F分别在边AC、BC、AB上,如果AC=10,BC=6,那么正方形DCEF的边长为 如图,AB为⊙O的一条弦,CD为直径(C不与A、B及
如图,AB为⊙O的一条弦,CD为直径(C不与A、B及

 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,若关于x的一元二次方程ax2+bx+c+m=0有实数根,则m的取值范围是
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,若关于x的一元二次方程ax2+bx+c+m=0有实数根,则m的取值范围是