题目内容
10.用加减法解下列方程组:(1)$\left\{\begin{array}{l}{3m-2n=5}\\{4m+2n=9}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x-5y=7}\\{4x+2y=5}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组变形后,利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{3m-2n=5①}\\{4m+2n=9②}\end{array}\right.$,
①+②得:7m=14,即m=2,
把m=2代入①得:n=$\frac{1}{2}$,
则方程组的解为$\left\{\begin{array}{l}{m=2}\\{n=\frac{1}{2}}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{3x-5y=7①}\\{4x+2y=5②}\end{array}\right.$,
①×2+②×5得:26x=39,即x=$\frac{3}{2}$,
把x=$\frac{3}{2}$代入②得:y=-$\frac{1}{2}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
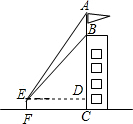 如图,为测量某建筑物BC上旗杆AB的高度,小明在距离建筑物BC底部11.4米的点F处,测得视线与水平线夹角∠AED=60°,∠BED=45°.小明的观测点与地面的距离EF为1.6米.
如图,为测量某建筑物BC上旗杆AB的高度,小明在距离建筑物BC底部11.4米的点F处,测得视线与水平线夹角∠AED=60°,∠BED=45°.小明的观测点与地面的距离EF为1.6米.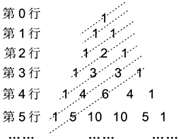 如图斜线方向所示,第12斜行各数的和是多少?
如图斜线方向所示,第12斜行各数的和是多少?