题目内容
7.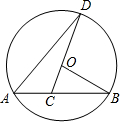 如图,AB是⊙O的弦,∠B=30°,C是弦AB上的一点,连结CO并延长CO交于点D,连结AD,若∠D=20°,则∠BOD=100°.
如图,AB是⊙O的弦,∠B=30°,C是弦AB上的一点,连结CO并延长CO交于点D,连结AD,若∠D=20°,则∠BOD=100°.
分析 连接OA,根据等腰三角形的性质求出∠OAB与∠OAD的度数,进而可得出结论.
解答 解:连接OA,
∵OA=OB,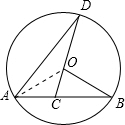
∴∠OAB=∠B=30°,
∵OA=OD,
∴∠OAD=∠D=20°,
∴∠BAD=∠OAB+∠OAD=50°,
∴∠BOD=2∠BAD=100°,
故答案为:100.
点评 本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解答此题的关键.

练习册系列答案
相关题目
12.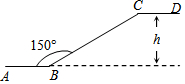 某商场一楼与二楼之间的手扶电梯如图所示.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
某商场一楼与二楼之间的手扶电梯如图所示.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
 某商场一楼与二楼之间的手扶电梯如图所示.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
某商场一楼与二楼之间的手扶电梯如图所示.其中AB、CD分别表示一楼、二楼地面的水平线,∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )| A. | 4$\sqrt{3}$m | B. | 8m | C. | $\frac{8}{3}$$\sqrt{3}$m | D. | 4m |
19.x7可以表示为( )
| A. | x3+x4 | B. | x3•x4 | C. | x14÷x2 | D. | (x3)4 |
17.公式L=L0+KP表示当重力为P时的物体作用在弹簧上时弹簧的长度,L0代表弹簧的初始长度,用厘米(cm)表示,K表示单位重力物体作用在弹簧上时弹簧拉伸的长度,用厘米(cm)表示.下面给出的四个公式中,表明这是一个短而硬的弹簧的是( )
| A. | L=10+0.5P | B. | L=10+5P | C. | L=80+0.5P | D. | L=80+5P |
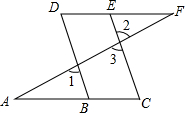 完成下列推理过程
完成下列推理过程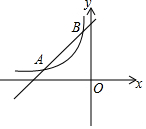 如图,直线y=kx+b与双曲线$y=\frac{m}{x}$(x<0)相交于A(-4,a)、B(-1,4)两点.
如图,直线y=kx+b与双曲线$y=\frac{m}{x}$(x<0)相交于A(-4,a)、B(-1,4)两点.