题目内容
10.先化简,再在-3,-1,0,$\sqrt{2}$,2中选择一个合适的x值代入求值.$\frac{{x}^{2}}{x+3}$•$\frac{{x}^{2}-9}{{x}^{2}-2x}$$+\frac{x}{x-2}$.
分析 根据分式的乘法和加法可以化简题目中的式子,然后在-3,-1,0,$\sqrt{2}$,2中选择一个使得原分式有意义的x的值代入即可解答本题.
解答 解:$\frac{{x}^{2}}{x+3}$•$\frac{{x}^{2}-9}{{x}^{2}-2x}$$+\frac{x}{x-2}$
=$\frac{{x}^{2}}{x+3}•\frac{(x+3)(x-3)}{x(x-2)}+\frac{x}{x-2}$
=$\frac{x(x-3)}{x-2}+\frac{x}{x-2}$
=$\frac{{x}^{2}-3x+x}{x-2}$
=$\frac{x(x-2)}{x-2}$
=x,
当x=-1时,原式=-1.
点评 本题考查分式的化简求值,解答本题的关键是明确分式的化简求值的方法.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
18. 如图所示,已知AB∥CD,下列结论正确的是( )
如图所示,已知AB∥CD,下列结论正确的是( )
 如图所示,已知AB∥CD,下列结论正确的是( )
如图所示,已知AB∥CD,下列结论正确的是( )| A. | ∠1=∠2 | B. | ∠2=∠3 | C. | ∠1=∠4 | D. | ∠3=∠4 |
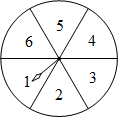 如图,转盘中6个扇形的面积相等,任意转动转盘1次,当转盘停止转动时,指针指向的数小于5的概率为$\frac{2}{3}$.
如图,转盘中6个扇形的面积相等,任意转动转盘1次,当转盘停止转动时,指针指向的数小于5的概率为$\frac{2}{3}$.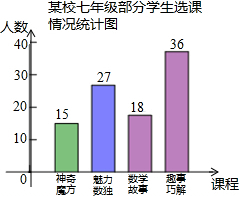 为培养学生数学学习兴趣,某校七年级准备开设“神奇魔方”、“魅力数独”、“数学故事”、“趣题巧解”四门选修课(每位学生必须且只选其中一门).
为培养学生数学学习兴趣,某校七年级准备开设“神奇魔方”、“魅力数独”、“数学故事”、“趣题巧解”四门选修课(每位学生必须且只选其中一门).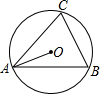 如图,△ABC内接于⊙O,若∠OAB=32°,则∠C=58°.
如图,△ABC内接于⊙O,若∠OAB=32°,则∠C=58°.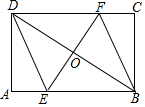 如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.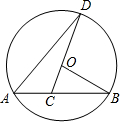 如图,AB是⊙O的弦,∠B=30°,C是弦AB上的一点,连结CO并延长CO交于点D,连结AD,若∠D=20°,则∠BOD=100°.
如图,AB是⊙O的弦,∠B=30°,C是弦AB上的一点,连结CO并延长CO交于点D,连结AD,若∠D=20°,则∠BOD=100°.