题目内容
6.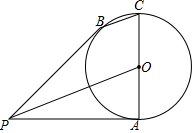 如图,已知线段AC为⊙O的直径,PA为⊙O的切线,切点为A,B为⊙O上一点,且BC∥PO.
如图,已知线段AC为⊙O的直径,PA为⊙O的切线,切点为A,B为⊙O上一点,且BC∥PO.(1)求证:PB为⊙O的切线;
(2)若⊙O的半径为1,PA=3,求BC的长.
分析 (1)连接OB,根据平行线的想知道的∠POA=∠BCA,根据全等三角形的性质得到∠PBO=∠PAO,根据切线的性质得到∠PAO=90°,于是得到结论;
(2)过O作OH⊥BC于H,则CH=$\frac{1}{2}$BC,根据勾股定理得到OP=$\sqrt{10}$,解直角三角形即可得到结论.
解答 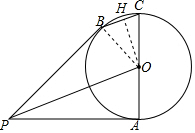 (1)证明:连接OB,
(1)证明:连接OB,
∵∠BCA=$\frac{1}{2}∠AOB$,
又∵BC∥OP,
∴∠POA=∠BCA,
∴∠POA=∠BOP,
在△AOP与△BOP中,$\left\{\begin{array}{l}{OA=OB}\\{∠POA=∠BOP}\\{OP=OP}\end{array}\right.$,
∴△AOP≌△BOP,
∴∠PBO=∠PAO,
又∵PA为⊙O的切线,
∴∠PAO=90°,
∴∠OBP=90°,
又OB为⊙O的半径,
∴PB为⊙O的切线;
(2)解:过O作OH⊥BC于H,则CH=$\frac{1}{2}$BC,
在Rt△AOP中,OP2=PA2+OA2=32+12=10,
又∵OP>0,
∴OP=$\sqrt{10}$,
∵∠POA=∠BCA,
∴cos∠BCA=cos∠POA=$\frac{1}{{\sqrt{10}}}$,
在Rt△OHC中,OC=1,cos∠BCA=$\frac{CH}{OC}$即$\frac{1}{{\sqrt{10}}}=\frac{CH}{1}$,
∴CH=$\frac{{\sqrt{10}}}{10}$,
∴BC=2CH=$\frac{{\sqrt{10}}}{5}$.
点评 本题考查了切线的判定和性质,解直角三角形,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
15.长沙磁浮快线2016年5月6日上午载客试运营.这是我国首条完全拥有自主知识产权的中低速磁浮商业运营铁路,标志着中国磁浮技术实现了从研发到应用的全覆盖,成为世界上少数几个掌握该项技术的国家之一.该工程总投资42.9亿元,则数据42.9亿用科学记数法表示为( )
| A. | 42.9×108 | B. | 4.29×108 | C. | 4.29×109 | D. | 4.3×109 |
16.下列各式能用平方差公式计算的是( )
| A. | (3a+b)(a-b) | B. | (3a+b)(-3a-b) | C. | (-3a-b)(-3a+b) | D. | (-3a+b)(3a-b) |
 如图,在?ABCD中,∠BAD的平分线AE交DC于点E,若∠DAE=25°,求∠C、∠B的度数.
如图,在?ABCD中,∠BAD的平分线AE交DC于点E,若∠DAE=25°,求∠C、∠B的度数.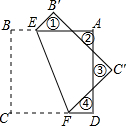 如图,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③④四个三角形的周长之和为32.
如图,正方形纸片ABCD的边长为8,将其沿EF折叠,则图中①②③④四个三角形的周长之和为32.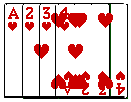 将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上,从中随机抽取两张.
将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上,从中随机抽取两张. 如图,在△ABC和△AEF中,AC∥EF,AB=FE,AC=AF,求证:∠B=∠E.
如图,在△ABC和△AEF中,AC∥EF,AB=FE,AC=AF,求证:∠B=∠E.