题目内容
11.计算:(1)$\sqrt{12}$+$\sqrt{27}$×$\sqrt{18}$
(2)2$\sqrt{2}$-3$\sqrt{3}$+$\sqrt{2}$-$\sqrt{3}$-3$\sqrt{2}$
(3)($\sqrt{11}$+$\frac{\sqrt{22}}{\sqrt{11}}$)2.
分析 (1)根据二次根式的混合运算顺序,首先计算乘法,然后计算加法,求出算式$\sqrt{12}$+$\sqrt{27}$×$\sqrt{18}$的值是多少即可.
(2)应用加法交换律和结合律,求出算式2$\sqrt{2}$-3$\sqrt{3}$+$\sqrt{2}$-$\sqrt{3}$-3$\sqrt{2}$的值是多少即可.
(3)首先把$\sqrt{11}$+$\frac{\sqrt{22}}{\sqrt{11}}$化成$\sqrt{11}$+$\sqrt{2}$,然后求出$\sqrt{11}+\sqrt{2}$的平方是多少即可.
解答 解:(1)$\sqrt{12}$+$\sqrt{27}$×$\sqrt{18}$
=2$\sqrt{3}$$+3\sqrt{3}$×$3\sqrt{2}$
=2$\sqrt{3}$+9$\sqrt{6}$
(2)2$\sqrt{2}$-3$\sqrt{3}$+$\sqrt{2}$-$\sqrt{3}$-3$\sqrt{2}$
=(2$\sqrt{2}$+$\sqrt{2}$-3$\sqrt{2}$)+(-3$\sqrt{3}$-$\sqrt{3}$)
=0-4$\sqrt{3}$
=-4$\sqrt{3}$
(3)($\sqrt{11}$+$\frac{\sqrt{22}}{\sqrt{11}}$)2
=($\sqrt{11}$+$\sqrt{2}$)2
=11$+2\sqrt{22}$+2
=13+2$\sqrt{22}$
点评 此题主要考查了二次根式的混合运算,要熟练掌握,解答此题的关键是要明确:①与有理数的混合运算一致,运算顺序先乘方再乘除,最后加减,有括号的先算括号里面的.②在运算中每个根式可以看做是一个“单项式”,多个不同类的二次根式的和可以看作“多项式”.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案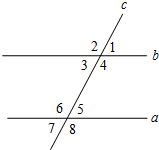 如图,直线a,b都与直线c相交,给出下列条件:
如图,直线a,b都与直线c相交,给出下列条件:①∠1=∠5;②∠3=∠5;③∠1=∠6;④∠2=∠7;⑤∠4=∠8.
其中,能够得出a∥b的条件是( )
| A. | ①②⑤ | B. | ②③⑤ | C. | ③④⑤ | D. | ①②④ |
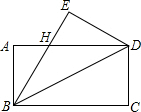 如图,将一块长方形的纸片ABCD沿BD翻折后,点C与E重合,若∠ADB=30°,EH=4cm,则BC的长度为( )
如图,将一块长方形的纸片ABCD沿BD翻折后,点C与E重合,若∠ADB=30°,EH=4cm,则BC的长度为( )| A. | 10cm | B. | 12cm | C. | 13cm | D. | 14cm |
| A. | 3 | B. | -4 | C. | -1 | D. | 7 |