题目内容
8. 如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.
如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C.(1)求证:AB=AC.
(2)若PC=2$\sqrt{5}$,求⊙O的半径.
分析 (1)由同圆半径相等和对顶角相等得∠OBP=∠APC,由圆的切线性质和垂直得∠ABP+∠OBP=90°和∠ACB+∠APC=90°,则∠ABP=∠ACB,根据等角对等边得AB=AC;
(2)设⊙O的半径为r,分别在Rt△AOB和Rt△ACP中根据勾股定理列等式,并根据AB=AC得52-r2=(2$\sqrt{5}$)2-(5-r)2,求出r的值即可.
解答 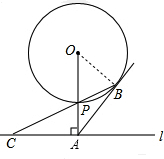 证明:(1)连接OB,
证明:(1)连接OB,
∵OB=OP,
∴∠OPB=∠OBP,
∵∠OPB=∠APC,
∴∠OBP=∠APC,
∵AB与⊙O相切于点B,
∴OB⊥AB,
∴∠ABO=90°,
∴∠ABP+∠OBP=90°,
∵OA⊥AC,
∴∠OAC=90°,
∴∠ACB+∠APC=90°,
∴∠ABP=∠ACB,
∴AB=AC;
(2)设⊙O的半径为r,
在Rt△AOB中,AB2=OA2-OB2=52-r2,
在Rt△ACP中,AC2=PC2-PA2,
AC2=(2$\sqrt{5}$)2-(5-r)2,
∵AB=AC,
∴52-r2=(2$\sqrt{5}$)2-(5-r)2,
解得:r=3,
则⊙O的半径为3.
点评 本题考查了圆的切线的性质,圆的切线垂直于经过切点的半径;并利用勾股定理列等式,求圆的半径;此类题的一般做法是:若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系;简记作:见切点,连半径,见垂直.

练习册系列答案
相关题目
19.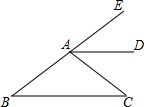 如图,AD是∠EAC的平分线,AD∥BC,∠B=28°,则∠C为( )
如图,AD是∠EAC的平分线,AD∥BC,∠B=28°,则∠C为( )
 如图,AD是∠EAC的平分线,AD∥BC,∠B=28°,则∠C为( )
如图,AD是∠EAC的平分线,AD∥BC,∠B=28°,则∠C为( )| A. | 28° | B. | 56° | C. | 14° | D. | 124° |
20.计算:(-2a3)2÷a2的正确结果是( )
| A. | -4a4 | B. | 4a4 | C. | -4a8 | D. | 4a8 |
16. 如图,在△ABC中,∠C=Rt∠,AB=5,AC=4,则sinA的值是( )
如图,在△ABC中,∠C=Rt∠,AB=5,AC=4,则sinA的值是( )
 如图,在△ABC中,∠C=Rt∠,AB=5,AC=4,则sinA的值是( )
如图,在△ABC中,∠C=Rt∠,AB=5,AC=4,则sinA的值是( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{5}{3}$ |
3.给出四个数0,-1,$\sqrt{2}$,1,其中最大的数是( )
| A. | 0 | B. | -1 | C. | $\sqrt{2}$ | D. | 1 |
19.在平面直角坐标系中,将抛物线y=-$\frac{1}{2}$x2向下平移1个单位长度,再向左平移1个单位长度,得到的抛物线的解析式是( )
| A. | y=-$\frac{1}{2}$x2-x-$\frac{3}{2}$ | B. | y=-$\frac{1}{2}$x2+x-$\frac{1}{2}$ | C. | y=-$\frac{1}{2}$x2+x-$\frac{3}{2}$ | D. | y=-$\frac{1}{2}$x2-x-$\frac{1}{2}$ |
15.下列运算正确的是( )
| A. | -2x2y•3xy2=-6x2y2 | B. | (-x-2y)(x+2y)=x2-4y2 | ||
| C. | 6x3y2÷2x2y=3xy | D. | (4x3y2)2=16x9y4 |

 ,
,  相交于点
相交于点 ,
,  平分
平分 ;若
;若 ,求
,求 的度数.
的度数.