题目内容
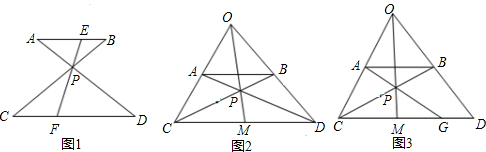
（1）如图1，AB∥CD，AD与BC交于点P，过P点的直线与AB、CD分别交于E，F．求证：
=
（2）如图2，在图1中，连接CA、DB并延长相交于O，连接OP并延长交CD于M，求证：点M为CD的中点；
（3）如图3，在图2中，若点G从D点向左移动（不与C点重合），AG与BC交于点P，连OP并延长交CD于M，直接写出MC、MG、MD之间的关系式．
| AE |
| BE |
| DF |
| CF |
（2）如图2，在图1中，连接CA、DB并延长相交于O，连接OP并延长交CD于M，求证：点M为CD的中点；
（3）如图3，在图2中，若点G从D点向左移动（不与C点重合），AG与BC交于点P，连OP并延长交CD于M，直接写出MC、MG、MD之间的关系式．
考点：相似三角形的判定与性质
专题：
分析：（1）如图1，先由相似三角形的判定定理得出△AEP∽△DFP，△BEP∽△CFP，根据相似三角形对应边成比例得到
=
，
=
，等量代换后得出
=
，然后根据比例的性质证明出
=
；
（2）如图2，设OM交AB于点N．先由相似三角形的判定定理得出△AON∽△COM，△BON∽△DOM，△AOB∽△COD，根据相似三角形对应边成比例得到
=
，
=
，
=
，等量代换后得出
=
①，再由△ANP∽△DMP，△BNP∽△CMP，△APB∽△DPC，得出
=
，
=
，
=
，则
=
②，然后将①式除以②式得出
=
，进而得到CM=DM；
（3）如图3，设OM交AB于点N．先由相似三角形的判定定理得出△MCP∽△NBP，△NAP∽△MGP，根据相似三角形对应边成比例得到
=
①，
=
②，将①×②，得出
×
=
×
=1，即
=
．又△AON∽△COM，△BON∽△DOM，则
=
，
=
，等量代换后得出
=
，根据比例的性质得出
=
，于是由等量代换得出
=
，进而求出MC、MG、MD之间的关系式为MC2=MG•MD．
| AE |
| DF |
| EP |
| FP |
| BE |
| CF |
| EP |
| FP |
| AE |
| DF |
| BE |
| CF |
| AE |
| BE |
| DF |
| CF |
（2）如图2，设OM交AB于点N．先由相似三角形的判定定理得出△AON∽△COM，△BON∽△DOM，△AOB∽△COD，根据相似三角形对应边成比例得到
| OA |
| OC |
| AN |
| CM |
| OB |
| OD |
| BN |
| DM |
| OA |
| OC |
| OB |
| OD |
| AN |
| CM |
| BN |
| DM |
| AN |
| DM |
| AP |
| DP |
| BN |
| CM |
| BP |
| CP |
| AP |
| DP |
| BP |
| CP |
| AN |
| DM |
| BN |
| CM |
| DM |
| CM |
| CM |
| DM |
（3）如图3，设OM交AB于点N．先由相似三角形的判定定理得出△MCP∽△NBP，△NAP∽△MGP，根据相似三角形对应边成比例得到
| MC |
| NB |
| MP |
| NP |
| NA |
| MG |
| NP |
| MP |
| MC |
| NB |
| NA |
| MG |
| MP |
| NP |
| NP |
| MP |
| MC |
| MG |
| NB |
| NA |
| NA |
| MC |
| ON |
| OM |
| NB |
| MD |
| ON |
| OM |
| NA |
| MC |
| NB |
| MD |
| MD |
| MC |
| NB |
| NA |
| MC |
| MG |
| MD |
| MC |
解答：（1）证明：如图1，∵AB∥CD，AD与BC交于点P，
∴△AEP∽△DFP，△BEP∽△CFP，
∴
=
，
=
，
∴
=
，
∴
=
；
（2）证明：如图2，设OM交AB于点N．
∵AB∥CD，
∴△AON∽△COM，△BON∽△DOM，△AOB∽△COD，
∴
=
，
=
，
=
，
∴
=
①，
∵△ANP∽△DMP，△BNP∽△CMP，△APB∽△DPC，
∴
=
，
=
，
=
，
∴
=
②，
①÷②，
=
，
∴CM=DM，即点M为CD的中点；
（3）解：MC2=MG•MD，理由如下：
如图3，设OM交AB于点N．
∵AB∥CD，
∴△MCP∽△NBP，△NAP∽△MGP，
∴
=
①，
=
②，
①×②，得
×
=
×
=1，
∴
=
．
∵△AON∽△COM，△BON∽△DOM，
∴
=
，
=
，
∴
=
，
∴
=
，
∴
=
，
∴MC2=MG•MD．
∴△AEP∽△DFP，△BEP∽△CFP，
∴
| AE |
| DF |
| EP |
| FP |
| BE |
| CF |
| EP |
| FP |
∴
| AE |
| DF |
| BE |
| CF |
∴
| AE |
| BE |
| DF |
| CF |
（2）证明：如图2，设OM交AB于点N．
∵AB∥CD，
∴△AON∽△COM，△BON∽△DOM，△AOB∽△COD，
∴
| OA |
| OC |
| AN |
| CM |
| OB |
| OD |
| BN |
| DM |
| OA |
| OC |
| OB |
| OD |
∴
| AN |
| CM |
| BN |
| DM |
∵△ANP∽△DMP，△BNP∽△CMP，△APB∽△DPC，
∴
| AN |
| DM |
| AP |
| DP |
| BN |
| CM |
| BP |
| CP |
| AP |
| DP |
| BP |
| CP |
∴
| AN |
| DM |
| BN |
| CM |
①÷②，
| DM |
| CM |
| CM |
| DM |
∴CM=DM，即点M为CD的中点；
（3）解：MC2=MG•MD，理由如下：如图3，设OM交AB于点N．
∵AB∥CD，
∴△MCP∽△NBP，△NAP∽△MGP，
∴
| MC |
| NB |
| MP |
| NP |
| NA |
| MG |
| NP |
| MP |
①×②，得
| MC |
| NB |
| NA |
| MG |
| MP |
| NP |
| NP |
| MP |
∴
| MC |
| MG |
| NB |
| NA |
∵△AON∽△COM，△BON∽△DOM，
∴
| NA |
| MC |
| ON |
| OM |
| NB |
| MD |
| ON |
| OM |
∴
| NA |
| MC |
| NB |
| MD |
∴
| MD |
| MC |
| NB |
| NA |
∴
| MC |
| MG |
| MD |
| MC |
∴MC2=MG•MD．
点评：本题考查了相似三角形的判定与性质，比例的性质，难度适中．题中需要多次运用相似三角形对应边的比，找准中间过渡比是解题的关键．
练习册系列答案
相关题目
在平面直角坐标系中，已知点A（3，0）、B（3，4）是以AB为边的正方形ABCD的两个顶点，如图所示．
如图，将矩形ABCD沿AE向上折叠，使点B落在DC边上的F处，若△AFD的周长为9，△ECF的周长为3，则矩形ABCD的周长为