题目内容
9. 如图,E,F分别在△ABC的边上,且EF∥DG是BC延长线上一点,下列结论错误的是( )
如图,E,F分别在△ABC的边上,且EF∥DG是BC延长线上一点,下列结论错误的是( )| A. | ∠ACD>∠AEF | B. | ∠AFD>∠AEF+∠A | C. | ∠D>∠AFE-∠CFD | D. | ∠AFE=∠CFD+∠D |
分析 先根据直线平行的性质得到∠AEF=∠B,∠AFE=∠ACB,然后根据三角形外角的性质进行判断即可.
解答 解:∵EF∥BC,
∴∠AEF=∠B,∠AFE=∠ACB,
∵∠ACD>∠B,
∴∠ACD>∠AEF,所以A选项正确;
∵∠AFD>∠ACD,
而∠ACD=∠B+∠A=∠AEF+∠A,
∴∠AFD>∠AEF+∠A,所以B选项正确;
∵∠ACD+∠ACB=180°,
∴∠ACD+∠AFE=180°,所以C选项错误;
∵∠AFE=∠ACB=∠CFD+∠D,
所以D选项正确.
故选C.
点评 本题考查了三角形外角的性质:三角形任意一外角等于与之不相邻两内角的和;三角形任意一外角大于与之不相邻任意一内角.也考查了直线平行的性质.

练习册系列答案
相关题目
20. 如图,?ABCD的对角线AC、BD相交于点O,点E是CD的中点,△ABD的周长为8cm,则△DOE的周长是( )
如图,?ABCD的对角线AC、BD相交于点O,点E是CD的中点,△ABD的周长为8cm,则△DOE的周长是( )
 如图,?ABCD的对角线AC、BD相交于点O,点E是CD的中点,△ABD的周长为8cm,则△DOE的周长是( )
如图,?ABCD的对角线AC、BD相交于点O,点E是CD的中点,△ABD的周长为8cm,则△DOE的周长是( )| A. | 8cm | B. | 6cm | C. | 4cm | D. | 2cm |
18. 如图,△ABC中,AB=AC=10,DE是AB的中垂线,△BCD的周长为16,则BC的长为( )
如图,△ABC中,AB=AC=10,DE是AB的中垂线,△BCD的周长为16,则BC的长为( )
 如图,△ABC中,AB=AC=10,DE是AB的中垂线,△BCD的周长为16,则BC的长为( )
如图,△ABC中,AB=AC=10,DE是AB的中垂线,△BCD的周长为16,则BC的长为( )| A. | 5 | B. | 6 | C. | 8 | D. | 10 |
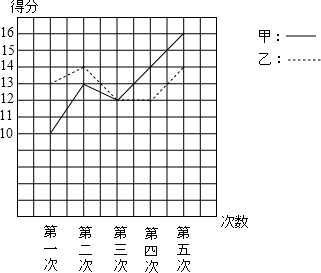 如图是甲、乙两位同学参加某体育项目训练,近期五次测试成绩得分情况.
如图是甲、乙两位同学参加某体育项目训练,近期五次测试成绩得分情况. 解不等式组$\left\{\begin{array}{l}{2x>3x-2}\\{\frac{2x-1}{3}≥\frac{1}{2}x-\frac{2}{3}}\end{array}\right.$.
解不等式组$\left\{\begin{array}{l}{2x>3x-2}\\{\frac{2x-1}{3}≥\frac{1}{2}x-\frac{2}{3}}\end{array}\right.$.