题目内容
17.两个同学对问题“若方程组$\left\{\begin{array}{l}3{a_1}x+2{b_1}y=5{c_1}\;,\;\;\\ 3{a_2}x+2{b_2}y=5{c_2}\end{array}\right.$的解是$\left\{\begin{array}{l}x=3\;,\;\;\\ y=4\;,\;\;\end{array}\right.$求方程组$\left\{\begin{array}{l}{a_1}x+{b_1}y={c_1}\;,\;\;\\{a_2}x+{b_2}x={c_2}\end{array}\right.$的解.”提出各自的想法.甲说:“这个题目好像条件不够,不能求解”.乙说:“它们的系数有一定的规律,可以试试”.参考他们的讨论,你认为这个题目的解应该是多少?分析 所求方程组整理后,仿照已知方程组的解确定出解即可.
解答 解:方程组可以化为$\left\{\begin{array}{l}{a_1}\frac{3x}{5}+{b_1}\frac{2y}{5}={c_1}\\{a_2}\frac{3x}{5}+{b_2}\frac{2y}{5}={c_2}\end{array}\right.$,
所以$\left\{\begin{array}{l}{a_1}x+{b_1}y={c_1}\\{a_2}x+{b_2}x={c_2}\end{array}\right.$的解为$\left\{\begin{array}{l}x=\frac{3}{5}×3=\frac{9}{5}\\ y=\frac{2}{5}×4=\frac{8}{5}\end{array}\right.$.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
8.“東星時代广場”六个字中,是轴对称图形的是( )
| A. | 東 | B. | 星 | C. | 時 | D. | 場 |
9. 如图,E,F分别在△ABC的边上,且EF∥DG是BC延长线上一点,下列结论错误的是( )
如图,E,F分别在△ABC的边上,且EF∥DG是BC延长线上一点,下列结论错误的是( )
 如图,E,F分别在△ABC的边上,且EF∥DG是BC延长线上一点,下列结论错误的是( )
如图,E,F分别在△ABC的边上,且EF∥DG是BC延长线上一点,下列结论错误的是( )| A. | ∠ACD>∠AEF | B. | ∠AFD>∠AEF+∠A | C. | ∠D>∠AFE-∠CFD | D. | ∠AFE=∠CFD+∠D |
6.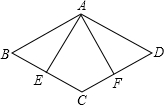 菱形ABCD中,如图,AE⊥BC于E,AF⊥CD于F,若BE=EC,则∠EAF=( )
菱形ABCD中,如图,AE⊥BC于E,AF⊥CD于F,若BE=EC,则∠EAF=( )
 菱形ABCD中,如图,AE⊥BC于E,AF⊥CD于F,若BE=EC,则∠EAF=( )
菱形ABCD中,如图,AE⊥BC于E,AF⊥CD于F,若BE=EC,则∠EAF=( )| A. | 75° | B. | 60° | C. | 50° | D. | 45° |
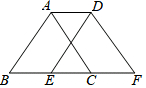 如图,将边长为2cm的等边△ABC沿边BC向右平移1cm得到△DEF,则四边形ABFD的周长为8cm.
如图,将边长为2cm的等边△ABC沿边BC向右平移1cm得到△DEF,则四边形ABFD的周长为8cm. 计算下面圆锥体的体积.(单位:厘米)
计算下面圆锥体的体积.(单位:厘米)