题目内容
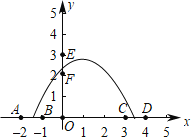
【题目】如图,在一个与地面垂直的截面中建立直角坐标系(横坐标表示地面位移,纵坐标表示高度),一架无人机的飞行路线为y=ax2+bx+c(a≠0),在直角坐标系中x轴上的线段AB上的某点起飞,途经空中线段EF上的某点,最后在线段CD上的某点降落,其中A(﹣2,0)、B(﹣1,0)、C(3,0)、D(4,0)、E(0,3)、F(0,2),则下列结论正确的有_____(填序号)
(1)abc<0;
(2)从起飞到当x≤1时无人机一直是上升的;
(3)2≤a+b+c≤4.5;
(4)最大飞行高度不超过4.
【答案】(1)(4)
【解析】
由抛物线的开口方向可判断a,由抛物线与y轴的交点可判断c,由对称性可得b的正负,进而可判断(1);
取起飞点A与降落点C,可得抛物线的对称轴,然后根据抛物线的性质可判断(2);
由图象可知,当抛物线过点B,点E,点C时,飞行高度最大,利用待定系数法求出此时的抛物线的解析式,从而可判断(3)(4)的正误.
解:∵由题意可知,抛物线开口向下,且抛物线的对称轴位于y轴右侧,
∴a<0,b>0,∵抛物线与y轴的交点在EF上,∴c>0,
∴abc<0,∴(1)正确;
当起飞点位于点A,而降落点位于点C时,对称轴为直线x=![]() <1,∴(2)不正确;
<1,∴(2)不正确;
由图象可知,当抛物线过点B,点E,点C时,飞行高度最大,
此时设y=a(x+1)(x﹣3),将E(0,3)代入得:3=a(0+1)(0﹣3),解得:a=﹣1,∴y=﹣(x+1)(x﹣3),
当x=1时,y=4,即最大飞行高度不超过4;故(4)正确,(3)不正确.
综上,(1)(4)正确.
故答案为:(1)(4).

练习册系列答案
相关题目