题目内容
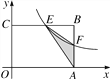
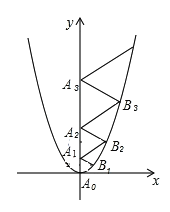
【题目】二次函数![]() 的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A2011在y轴的正半轴上,点B1,B2,B3,…,B2011在二次函数
的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A2011在y轴的正半轴上,点B1,B2,B3,…,B2011在二次函数![]() 位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2010B2011A2011都为等边三角形,则△A2010B2011A2011的边长=_____.
位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2010B2011A2011都为等边三角形,则△A2010B2011A2011的边长=_____.
【答案】2011
【解析】
分别过B1,B2,B3作y轴的垂线,垂足分别为A、B、C,设A0A1=a,A1A2=b,A2A3=c,则AB1![]() a,BB2
a,BB2![]() b,CB3
b,CB3![]() c,再根据所求正三角形的边长,分别表示B1,B2,B3的纵坐标,逐步代入抛物线y
c,再根据所求正三角形的边长,分别表示B1,B2,B3的纵坐标,逐步代入抛物线y![]() x2中,求a、b、c的值得出规律.
x2中,求a、b、c的值得出规律.
分别过B1,B2,B3作y轴的垂线,垂足分别为A、B、C.
设A0A1=a,A1A2=b,A2A3=c,则AB1![]() a,BB2
a,BB2![]() b,CB3
b,CB3![]() c,
c,
在正△A0B1A1中,B1(![]() a,
a,![]() ),
),
代入y![]() x2中,得
x2中,得![]() (
(![]() a)2,解得:a=1或a=0(舍去),即A0A1=1,
a)2,解得:a=1或a=0(舍去),即A0A1=1,
在正△A1B2A2中,B2(![]() b,1
b,1![]() ),
),
代入y![]() x2中,得1
x2中,得1![]() (
(![]() b)2,解得:b=2或b=-1(舍去),即A1A2=2,
b)2,解得:b=2或b=-1(舍去),即A1A2=2,
在正△A2B3A3中,B3(![]() c,3
c,3![]() ),
),
代入y![]() x2中,得3
x2中,得3![]() (
(![]() c)2,解得:c=3或c=-2(舍去),即A2A3=3,
c)2,解得:c=3或c=-2(舍去),即A2A3=3,
由此可得△A2010B2011A2011的边长=2011.
故答案为:2011.


练习册系列答案
相关题目