Question

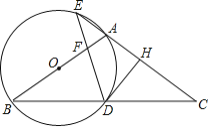
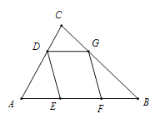
【题目】如图（1）是某公园里的一种健身器材，其侧面示意图如图（2）所示，其中AB=AC=120cm，BC=80cm，AD=30cm，∠DAC=90°．求点D到地面的高度是多少？

Answer 1

【答案】D到地面的高度为（10+）cm

【解析】

过A作AF⊥BC，垂足为F，过点D作DH⊥AF，垂足为H．先得出AF的长，再利用相似三角形的判定与性质得出AH的长即可得出答案．

解：过A作AF⊥BC，垂足为F，过点D作DH⊥AF，垂足为H．

∵AF⊥BC

∴BF=FC=BC=40cm．

根据勾股定理，得AF=（cm），

∵∠DHA=∠DAC=∠AFC=90°，

∴∠DAH+∠FAC=90°，∠C+∠FAC=90°，

∴∠DAH=∠C，

∴△DAH∽△ACF，

∴ ∴，

∴AH=10cm.

∴HF=（10+）cm ,

答：D到地面的高度为（10+）cm．

故答案为：D到地面的高度为（10+）cm.