题目内容
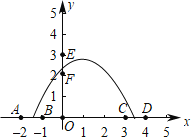
【题目】如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 为抛物线上一动点,过点
为抛物线上一动点,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.

(1)求抛物线的解析式.
(2)当点![]() 在直线
在直线![]() 下方的抛物线上运动时,求出
下方的抛物线上运动时,求出![]() 长度的最大值.
长度的最大值.
(3)当以![]() ,
,![]() ,
,![]() 为顶点的三角形是等腰三角形时,求此时
为顶点的三角形是等腰三角形时,求此时![]() 的值.
的值.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,线段
时,线段![]() 的长度有最大值,最大值为
的长度有最大值,最大值为![]() ;(3)
;(3)![]() 的值为6或
的值为6或![]() 或
或![]() 或3
或3
【解析】
(1)令![]() 即可得出点A的坐标,再根据点B的坐标利用待定系数法即可求得抛物线的解析式;
即可得出点A的坐标,再根据点B的坐标利用待定系数法即可求得抛物线的解析式;
(2)由点D的横坐标,可知点P和点D的坐标,再根据点![]() 在直线
在直线![]() 下方的抛物线上,即可表示PD解析式,并转化为顶点式就可得出答案;
下方的抛物线上,即可表示PD解析式,并转化为顶点式就可得出答案;
(3)根据题意分别表示出![]() ,
,![]() ,
,![]() 分当
分当![]() 时,当
时,当![]() 时,当
时,当![]() 时三种情况分别求出m的值即可.
时三种情况分别求出m的值即可.
(1)对于![]() ,取
,取![]() ,得
,得![]() ,∴
,∴![]() .
.
将![]() ,
,![]() 代入
代入![]() ,
,
得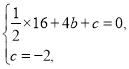 解得
解得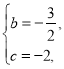
∴抛物线的解析式为![]() .
.
(2)∵点![]() 的横坐标为
的横坐标为![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∵点![]() 在直线
在直线![]() 下方的抛物线上,
下方的抛物线上,
∴![]()
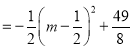 .
.
∵![]() ,
,
当![]() 时,线段
时,线段![]() 的长度有最大值,最大值为
的长度有最大值,最大值为![]() .
.
(3)由![]() ,
,![]() ,
,![]() ,得
,得![]() ,
,![]()
![]() ,
,![]() .
.
当![]() 为等腰三角形时,有三种情况:
为等腰三角形时,有三种情况:
①当![]() 时,
时,![]() ,即
,即![]() ,
,
解得![]() (不合题意,舍去),
(不合题意,舍去),![]() ;
;
②当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() ,
,![]() ;
;
③当![]() 时,
时,![]() ,即
,即![]() ,解得
,解得![]() .
.
综上所述,![]() 的值为6或
的值为6或![]() 或
或![]() 或3.
或3.

【题目】我市某公司用800万元购得某种产品的生产技术后,进一步投入资金1550万元购买生产设备,进行该产品的生产加工,已知生产这种产品每件还需成本费40元.经过市场调研发现:该产品的销售单价需要定在200元到300元之间较为合理.销售单价![]() (元)与年销售量
(元)与年销售量![]() (万件)之间的变化可近似的看作是如下表所反应的一次函数:
(万件)之间的变化可近似的看作是如下表所反应的一次函数:
销售单价 | 200 | 230 | 250 |
年销售量 | 14 | 11 | 9 |
(1)请求出![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(2)请说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最少亏损是多少?