题目内容
1.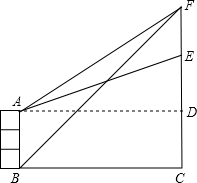 如图所示,楼房AB的对面有一个建筑物EC.建筑物上方有一个信号发射塔EF.为测量EF的高度,某数学活动小组在B处测得塔尖F仰角为45°.在A处测得塔尖F仰角为α、测得点E仰角为β.已知AB高为10米,求EF的高度.(参考数据:tanα=$\frac{3}{4}$,tanβ=$\frac{9}{25}$)
如图所示,楼房AB的对面有一个建筑物EC.建筑物上方有一个信号发射塔EF.为测量EF的高度,某数学活动小组在B处测得塔尖F仰角为45°.在A处测得塔尖F仰角为α、测得点E仰角为β.已知AB高为10米,求EF的高度.(参考数据:tanα=$\frac{3}{4}$,tanβ=$\frac{9}{25}$)
分析 通过解等腰直角△BFC得到BC=FC,结合矩形的性质推知AD=BC;然后通过解直角△AFD与直角△EAD分别求得AD的长度;最后利用AD的长度不变列出方程求得FD、ED的长度,则EF=FD-ED.
解答  解:依题意得,AD=BC.
解:依题意得,AD=BC.
∵在直角△BFC中,∠FBC=45°,则BC=FC.
∴AD=FC=10+FD.
∵在直角△AFD中,∠FAD=α,tanα=$\frac{3}{4}$,
∴$\frac{FD}{AD}$=$\frac{3}{4}$,则AD=$\frac{4}{3}$FD.
∴10+FD=$\frac{4}{3}$FD.
解得FD=30.
∴AD=40米
∵在直角△EAD中,∠EAD=β,tanβ=$\frac{9}{25}$,
∴$\frac{ED}{AD}$=$\frac{9}{25}$,即$\frac{ED}{40}$=$\frac{9}{25}$,
∴ED=$\frac{72}{5}$(米),
∴EF=FD-ED=30-$\frac{72}{5}$=$\frac{78}{5}$(米).
答:EF的长度是$\frac{78}{5}$米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
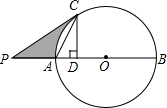 如图,已知⊙O的直径AB=10cm,C是⊙O上的一点,作CD⊥AB于点D,以C为顶点作∠PCA=∠ACD,交BA的延长线于点P,
如图,已知⊙O的直径AB=10cm,C是⊙O上的一点,作CD⊥AB于点D,以C为顶点作∠PCA=∠ACD,交BA的延长线于点P,