题目内容
将一张长为3,宽为1的矩形纸条和一张长为
,宽为2的矩形纸条交叉并重叠,使其重叠部分成为一个平行四边形,那么平行四边形周长的最大值是多少?
| 6 |
考点:矩形的性质,勾股定理,平行四边形的性质,相似三角形的判定与性质
专题:
分析:由两矩形的对角线相等,画出平行四边形周长最大时的图形,设DG=x,BG=y,由勾股定理列出方程求出x,y的值,代入周长公式求解即可.
解答:解:如图,

∵BE=3,DE=1,AD=
,AB=2,
∴矩形BFDE和ABCD的对角线相等,所以当在如图位置时周长最大,
设DG=x,BG=y,
∵∠A=∠E=90°,
∴△BAG∽△DEG,
∵DE=1,AB=2,
∴
=
=2,
∴y=2x,
由勾股定理得DE2-GE2=DE2,即x2-(3-y)2=1,①
BG2-AG2=AB2,即y2-(
-x)2=4②
解得x=
,y=
,
∴平行四边形周长的最大值为:2(x+y)=2(
+
)=12-2
.

∵BE=3,DE=1,AD=
| 6 |
∴矩形BFDE和ABCD的对角线相等,所以当在如图位置时周长最大,
设DG=x,BG=y,
∵∠A=∠E=90°,
∴△BAG∽△DEG,
∵DE=1,AB=2,
∴
| AB |
| DE |
| BG |
| DG |
∴y=2x,
由勾股定理得DE2-GE2=DE2,即x2-(3-y)2=1,①
BG2-AG2=AB2,即y2-(
| 6 |
解得x=
| 10 | ||
6+
|
| 20 | ||
6+
|
∴平行四边形周长的最大值为:2(x+y)=2(
| 10 | ||
6+
|
| 20 | ||
6+
|
| 6 |
点评:本题主要考查了矩形的性质,勾股定理,平行四边形的性质及相似三角形的判定与性质,解题的关键是正确的画出图形,利用勾股定理列出关系式.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
若点P为直线外一点,点A、B、C、D为直线l上的不同的点,其中PA=3,PB=4,PC=5,PD=3.那么点P到直线1的距离是( )
| A、小于3 | B、3 |
| C、不大于3 | D、不小于3 |
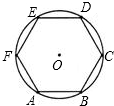 如图,已知正六边形ABCDEF的外接圆半径R=8cm,求四边形ABDE的面积.
如图,已知正六边形ABCDEF的外接圆半径R=8cm,求四边形ABDE的面积.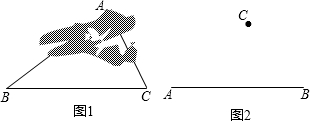
 如图,已知D、E分别为AB、AC上的点,AC=BC=BD,AD=AE,DE=CE,求∠B的度数.
如图,已知D、E分别为AB、AC上的点,AC=BC=BD,AD=AE,DE=CE,求∠B的度数.