题目内容
9.一般情况下$\frac{a}{3}$+$\frac{b}{6}$=$\frac{a+b}{3+6}$不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得$\frac{a}{3}$+$\frac{b}{6}$=$\frac{a+b}{3+6}$成立的一对数a,b为“相伴数对”,记为(a,b).(1)若(1,b)是“相伴数对”,求b的值;
(2)写出一个“相伴数对”(a,b),其中a≠0,且a≠1;
(3)若(m,n)是“相伴数对”,求代数式m-$\frac{27}{4}$n-[4m-2(3n-5)]的值.
分析 (1)利用题中的新定义确定出b的值即可;
(2)类比题中新定义得出一个“相伴数对”即可;
(3)利用题中新定义确定出m与n关系式,原式去括号合并后代入计算即可求出值.
解答 解:(1)根据题中新定义得:$\frac{1}{3}$+$\frac{b}{6}$=$\frac{b+1}{9}$,
解得:b=-4;
(2)答案不唯一,如(2.-8),满足$\frac{2}{3}$-$\frac{8}{6}$=$\frac{2-8}{3+6}$;
(3)∵$\frac{m}{3}$+$\frac{n}{6}$=$\frac{m+n}{3+6}$,∴n=-4m,
原式=m-$\frac{27}{4}$n-4m+6n-10,
∵n=-4m,
∴原式=m+27m-4m-24m-10=-10.
点评 此题考查了整式的加减-化简求值,以及有理数的混合运算,弄清题中的新定义是解本题的关键.

练习册系列答案
相关题目
10.已知二次函数y=ax2+bx+c的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数y=ax2+bx+c的图象上,则下列结论正确的是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y2<y1<y3 |
4.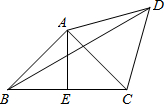 如图,四边形ABCD中,AB=AC=AD,E是BC的中点,AE=CE,∠BAC=3∠CBD,BD=6$\sqrt{2}$+6$\sqrt{6}$,则AB的长为( )
如图,四边形ABCD中,AB=AC=AD,E是BC的中点,AE=CE,∠BAC=3∠CBD,BD=6$\sqrt{2}$+6$\sqrt{6}$,则AB的长为( )
 如图,四边形ABCD中,AB=AC=AD,E是BC的中点,AE=CE,∠BAC=3∠CBD,BD=6$\sqrt{2}$+6$\sqrt{6}$,则AB的长为( )
如图,四边形ABCD中,AB=AC=AD,E是BC的中点,AE=CE,∠BAC=3∠CBD,BD=6$\sqrt{2}$+6$\sqrt{6}$,则AB的长为( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 12 | D. | 10$\sqrt{2}$ |
14.中百超市的收银台平均每小时有60名顾客前来排队付款,每个收银台每小时能应付80名顾客付款.某天某时刻,超市如果只开设一个收银台.付款开始2小时就没有顾客排队,如果当时就开设两个收银台,付款开始( )小时就没有人排队.
| A. | 1 | B. | 0.8 | C. | 0.6 | D. | 0.4 |
1.在Rt△ABC与Rt△A'B'C'中,∠C=∠C'=90°,∠A=∠B',AB=A'B',则下面结论正确的是( )
| A. | AB=A'C' | B. | BC=B'C' | C. | AC=B'C' | D. | ∠A=∠A' |
18.如图,已知点A表示的数是$\frac{1}{2}$,则点B表示的数是( )
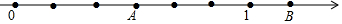
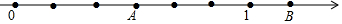
| A. | $1\frac{1}{3}$ | B. | $1\frac{1}{4}$ | C. | $1\frac{1}{5}$ | D. | $1\frac{1}{6}$ |
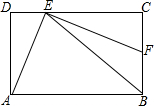 如图,在矩形ABCD中,BE平分∠ABC且交CD于点E,EF⊥AE且交BC于点F,求证:AE=EF.
如图,在矩形ABCD中,BE平分∠ABC且交CD于点E,EF⊥AE且交BC于点F,求证:AE=EF. 如图,AB是⊙O的直径,CD是⊙O的弦,求证:AE•BC=AD•CE.
如图,AB是⊙O的直径,CD是⊙O的弦,求证:AE•BC=AD•CE.