题目内容
6．四个各不相等的整数a、b、c、d，满足abcd=9，则a+b+c+d=（ ）| A． | 无法确定 | B． | 4 | C． | 10 | D． | 0 |
分析 根据有理数的乘法确定出a、b、c、d四个数，然后相加即可得解．
解答 解：∵1×（-1）×3×（-3）=9，
∴a、b、c、d四个数分别为±1，±3，
∴a+b+c+d=1+（-1）+3+（-3）=0．
故选D．
点评 本题考查了有理数的乘法，有理数的加法，是基础题，确定出a、b、c、d四个数的值是解题的关键．
练习册系列答案
相关题目
如图，AB是⊙O的直径，CD是⊙O的弦，求证：AE•BC=AD•CE．
14．中百超市的收银台平均每小时有60名顾客前来排队付款，每个收银台每小时能应付80名顾客付款．某天某时刻，超市如果只开设一个收银台．付款开始2小时就没有顾客排队，如果当时就开设两个收银台，付款开始（ ）小时就没有人排队．
| A． | 1 | B． | 0.8 | C． | 0.6 | D． | 0.4 |
1．在Rt△ABC与Rt△A'B'C'中，∠C=∠C'=90°，∠A=∠B'，AB=A'B'，则下面结论正确的是（ ）
| A． | AB=A'C' | B． | BC=B'C' | C． | AC=B'C' | D． | ∠A=∠A' |
11．
如图，△ABC中，DE∥BC，$\frac{AD}{BD}$=$\frac{1}{2}$，则OE：OB=（ ）
如图，△ABC中，DE∥BC，$\frac{AD}{BD}$=$\frac{1}{2}$，则OE：OB=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{1}{5}$ |
18．如图，已知点A表示的数是$\frac{1}{2}$，则点B表示的数是（ ）
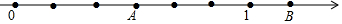
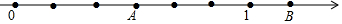
| A． | $1\frac{1}{3}$ | B． | $1\frac{1}{4}$ | C． | $1\frac{1}{5}$ | D． | $1\frac{1}{6}$ |
