题目内容
11. 如图,四边形ABCD的对角线AC与BD相交于点O,∠1=∠2,∠3=∠4.
如图,四边形ABCD的对角线AC与BD相交于点O,∠1=∠2,∠3=∠4.求证:(1)BC=DC; (2)AC⊥BD.
分析 (1)由∠1=∠2,∠3=∠4,再加AC为公共边可证△ABC≌△ADC,根据全等三角形的对应边相等即可解答;
(2)由(1)可得BC=DC,AB=AD,可得A、C都在BD的垂直平分线上,可得结论.
解答 解:(1)在△ABC和△ADC中,
$\left\{\begin{array}{l}{∠1=∠2}\\{AC=AC}\\{∠3=∠4}\end{array}\right.$,
∴△ABC≌△ADC(ASA),
∴BC=DC;
(2)由(1)知△ABC≌△ADC,
∴CB=CD,AB=AC,
∴点C、A在线段BD的垂直平分线上,
∴AC垂直平分BD.
点评 本题主要考查全等三角形的判定和性质及垂直平分线的判定,掌握判定的方法是解题的关键.

练习册系列答案
相关题目
19.方程(2x-5)(2x+3)=(2x-5)(x-4)的根是( )
| A. | x=$\frac{5}{2}$ | B. | x=-7 | C. | x1=$\frac{5}{2}$,x2=-7 | D. | 以上都不对 |
6.下列条件中,能作出唯一三角形的是( )
| A. | 已知两边 | B. | 已知两角 | C. | 已知两边一角 | D. | 已知两角一边 |
3.下列各式计算正确的是( )
| A. | a2+a2=2a4 | B. | a5-a2=a3 | C. | 3a+b=3ab | D. | -x2y+yx2=0 |
20.多项式3x2y-xy3+5xy-1是一个( )
| A. | 四次三项式 | B. | 三次三项式 | C. | 四次四项式 | D. | 三次四项式 |
 已知抛物线C1:y=-x2-2ax-2x-a2-3a+1的顶点在直线l上,
已知抛物线C1:y=-x2-2ax-2x-a2-3a+1的顶点在直线l上, 如图是由7个完全相同的小立方块搭成的几何体,已知每个小立方块的棱长为2cm.
如图是由7个完全相同的小立方块搭成的几何体,已知每个小立方块的棱长为2cm.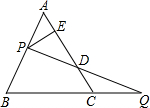 如图,过边长为6的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )
如图,过边长为6的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为( )