题目内容
16．若点（x1，y1），（x2，y2），（x3，y3）都是反比例函数y=-$\frac{2}{x}$图象上的点，且y1＜0＜y2＜y3，则x1、x2、x3的大小关系为x2＜x3＜x1．（请用“＜”连接）．分析 由点的坐标利用反比例函数图象上点的坐标特征即可找出x1、x2、x3，根据y1＜0＜y2＜y3，即可找出$\frac{-2}{{y}_{1}}$＞0＞$\frac{-2}{{y}_{3}}$＞$\frac{-2}{{y}_{2}}$，由此即可得出x2＜x3＜x1．
解答 解：∵点（x1，y1），（x2，y2），（x3，y3）都是反比例函数y=-$\frac{2}{x}$图象上的点，
∴x1=$\frac{-2}{{y}_{1}}$，x2=$\frac{-2}{{y}_{2}}$，x3=$\frac{-2}{{y}_{3}}$，
∵y1＜0＜y2＜y3，
∴$\frac{-2}{{y}_{1}}$＞0＞$\frac{-2}{{y}_{3}}$＞$\frac{-2}{{y}_{2}}$，
∴x2＜x3＜x1．
故答案为：x2＜x3＜x1．
点评 本题考查了反比例函数图象上点的坐标特征，根据反比例函数图象上点的坐标特征找出x1、x2、x3是解题的关键．
练习册系列答案
相关题目
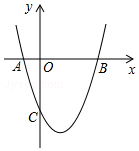如图，抛物线y=x2+bx+c与x轴交于A（-1，0），B（3，0）两点．
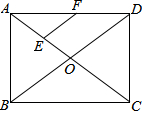如图，在矩形ABCD中，对角线AC．BD干H交于点O，点E．F分别是AO．AD中点，若AB=6，BC=8，则△AEF的周长为（ ）