题目内容
4.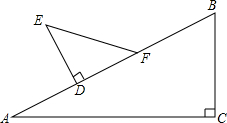 如图△ABC中,∠C=90°,∠A=30°,BC=5cm;△DEF中∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).
如图△ABC中,∠C=90°,∠A=30°,BC=5cm;△DEF中∠D=90°,∠E=45°,DE=3cm.现将△DEF的直角边DF与△ABC的斜边AB重合在一起,并将△DEF沿AB方向移动(如图).在移动过程中,D、F两点始终在AB边上(移动开始时点D与点A重合,一直移动至点F与点B重合为止).(1)当△DEF移动至什么位置,即AD的长为多少时,E、B的连线与AC平行?
(2)在△DEF的移动过程中,是否存在某个位置,使得∠EBD=22.5°?如果存在,求出AD的长度;如果
不存在,请说明理由.
分析 (1)连接EB,设BE∥AC,因为∠C=90°,∠A=30°,BC=5cm,所以AB=10cm,又因为∠FDE=90°,DE=3cm,所以DB=3$\sqrt{3}$cm,故AD的长度可求;
(2)当∠EBD=22.5°时,利用三角形外角的性质求得∠BEF=22.5°,则∠EBD=∠BEF,故BF=EF=3$\sqrt{2}$,AD=BD-BF-DF=7-3$\sqrt{2}$(cm).
解答 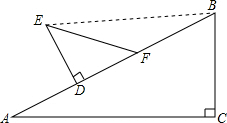 解:(1)AD=(10-3$\sqrt{3}$)cm时,BE∥AC.
解:(1)AD=(10-3$\sqrt{3}$)cm时,BE∥AC.
理由如下:连接EB,
设EB∥AC,则∠EBD=∠A=30°,
∵∠C=90°,∠A=30°,BC=5cm,
∴AB=10cm,
又∵∠FDE=90°,DE=3cm,
∴DB=3$\sqrt{3}$cm
∴AD=AB-BD=(10-3$\sqrt{3}$)cm,
∴AD=(10-3$\sqrt{3}$)cm时,BE∥AC;
(2)在△DEF的移动过程中,当AD=(7-3$\sqrt{3}$)cm时,使得∠EBD=22.5°.
理由如下:
假设∠EBD=22.5°.
∵在△DEF中,∠D=90°,∠DEF=45°,DE=3cm,
∴EF=3$\sqrt{2}$cm,∠DEF=∠DFE=45°,DE=DF=3cm.
又∵∠DFE=∠FEB+∠FBE=45°,
∴∠EBD=∠BEF,
∴BF=EF=3$\sqrt{2}$,
∴AD=AB-BF-DF=7-3$\sqrt{2}$(cm).
∴在△DEF的移动过程中,当AD=(7-3$\sqrt{2}$)cm时,使得∠EBD=22.5°.
点评 此题主要考查了勾股定理和锐角三角函数关系以及平行线的判定等知识,注意解题的方法不惟一,可让学生采用不同方法求解,培养学生的思维能力.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
16.2015年羊年除夕夜的10点半,在央视春晚送红包的活动中,微信“摇一摇”峰值的摇动次数达到8.1亿次/分钟,送出微信红包120 000 000个.将120 000 000用科学记数法表示应为( )
| A. | 0.12×109 | B. | 1.2×107 | C. | 1.2×108 | D. | 12×107 |
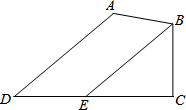 已知:如图,在四边形ABCD中,∠A=130°,∠C=90°,∠D=40°,BE∥AD交CD于点E.求证:BE平分∠ABC.
已知:如图,在四边形ABCD中,∠A=130°,∠C=90°,∠D=40°,BE∥AD交CD于点E.求证:BE平分∠ABC.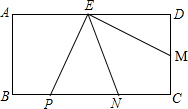 已知矩形ABCD中,AD=2AB,AB=6,E为AD中点,M为CD上一点,PE⊥EM交CB于点P,EN平分∠PEM交BC于点N.
已知矩形ABCD中,AD=2AB,AB=6,E为AD中点,M为CD上一点,PE⊥EM交CB于点P,EN平分∠PEM交BC于点N.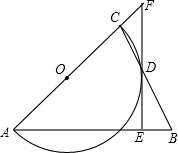 如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.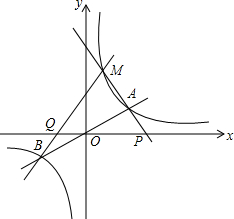 如图,已知双曲线y=$\frac{{k}_{1}+3}{x}$(k1为常数)与直线y=k2x(k2为常数)相交于A,B两点,双曲线在第一象限内部分有一点M(点M在A的左侧)在双曲线y=$\frac{{k}_{1}+3}{x}$上,设直线MA,MB分别与x轴分别交于P,Q两点.若MA=m•AP,MB=n•QB,则n-m的值是2.
如图,已知双曲线y=$\frac{{k}_{1}+3}{x}$(k1为常数)与直线y=k2x(k2为常数)相交于A,B两点,双曲线在第一象限内部分有一点M(点M在A的左侧)在双曲线y=$\frac{{k}_{1}+3}{x}$上,设直线MA,MB分别与x轴分别交于P,Q两点.若MA=m•AP,MB=n•QB,则n-m的值是2.