题目内容
18.在平面直角坐标系中,把点P(4,5)绕原点旋转90°得到点P1,则点P1的坐标是( )| A. | (5,-4) | B. | (-5,4) | C. | (5,-4)或(-5,4) | D. | (4,-5)或(-4,5) |
分析 作PQ⊥x轴于点Q,则OQ=45,PQ=5,于是把点旋转的问题转化为直角三角形旋转的问题,讨论:当把△OPQ绕原点逆时针旋转90°得到△OP′Q′,根据旋转的性质得P′Q′=PQ=5,OQ′=OQ=4,则P′(-5,4),当把△OPQ绕原点顺时针旋转90°得到△OP″Q″,同样方法易得P″(5,-4).
解答 解: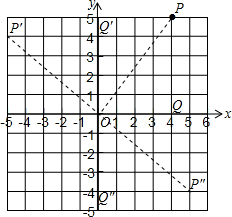 作PQ⊥x轴于点Q,则OQ=45,PQ=5,
作PQ⊥x轴于点Q,则OQ=45,PQ=5,
当把△OPQ绕原点逆时针旋转90°得到△OP′Q′,则P′Q′=PQ=5,OQ′=OQ=4,所以P′(-5,4),
当把△OPQ绕原点顺时针旋转90°得到△OP″Q″,同样方法可得P″(5,-4),
所以点P1的坐标是(-5,4)或(5,-4).
故选C.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
9.下列各式中,合并同类项正确的是( )
| A. | 6a-5a=1 | B. | 2a+3b=5ab | C. | 4x2y-5y2x=-x2y | D. | 13xy-13yx=0 |
10.计算2n+2•(-2)•(2n)2的结果为( )
| A. | -62n+1 | B. | -23n+2 | C. | -23n+3 | D. | -82n+3 |
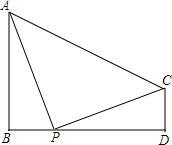 如图,已知AB丄BD,CD丄BD.
如图,已知AB丄BD,CD丄BD.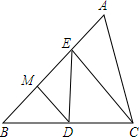 如图所示,已知△ABC面积为36,M为AB上的点,且BM:MA=1:2,MD∥EC,则△EBD的面积为12.
如图所示,已知△ABC面积为36,M为AB上的点,且BM:MA=1:2,MD∥EC,则△EBD的面积为12. 有理数a,b,c在数轴上对应如下图表示,则代数式|a+b|-|c-a|的化简结果是-b-c.
有理数a,b,c在数轴上对应如下图表示,则代数式|a+b|-|c-a|的化简结果是-b-c.