题目内容
7.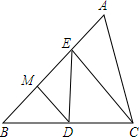 如图所示,已知△ABC面积为36,M为AB上的点,且BM:MA=1:2,MD∥EC,则△EBD的面积为12.
如图所示,已知△ABC面积为36,M为AB上的点,且BM:MA=1:2,MD∥EC,则△EBD的面积为12.
分析 连接CM,由BM:MA=1:2,得到BM:AB=1:3,于是得到S△BCM=$\frac{1}{3}{S}_{△ABC}$=12,根据MD∥EC,于是得到S△CDM=S△DME,即可得到距离.
解答 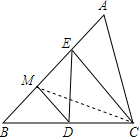 解:连接CM,
解:连接CM,
∵M为AB上的点,且BM:MA=1:2,
∴BM:AB=1:3,
∴S△BCM=$\frac{1}{3}{S}_{△ABC}$=12,
∵MD∥EC,
∴S△CDM=S△DME,
∴S△BDE=S△BCM=12.
故答案为:12.
点评 本题考查了三角形的面积,平行线间的距离,同底同高的三角形的面积相等,不同底但同高的三角形的面积吧比等于底的比,正确的作出辅助线是解题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
18.在平面直角坐标系中,把点P(4,5)绕原点旋转90°得到点P1,则点P1的坐标是( )
| A. | (5,-4) | B. | (-5,4) | C. | (5,-4)或(-5,4) | D. | (4,-5)或(-4,5) |
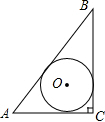 如图,在Rt△ABC中,∠C=90°,AB=5,△ABC为面积等于6,求△ABC的内切圆半径r.
如图,在Rt△ABC中,∠C=90°,AB=5,△ABC为面积等于6,求△ABC的内切圆半径r.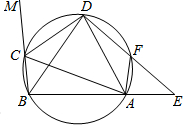 如图所示,圆内接四边形ABCD中,CD为∠ACB的外角的平分线,F为$\widehat{AD}$上一点,BC=AF,延长DF与BA的延长线交于E,求证:
如图所示,圆内接四边形ABCD中,CD为∠ACB的外角的平分线,F为$\widehat{AD}$上一点,BC=AF,延长DF与BA的延长线交于E,求证: 如图,已知∠ACE是ABC的一个外角,DC平分∠ACE,且AB∥CD,求证:△ABC为等腰三角形.
如图,已知∠ACE是ABC的一个外角,DC平分∠ACE,且AB∥CD,求证:△ABC为等腰三角形. 我们见过的瓶塞大都是圆柱形的.你见过一种“三用瓶塞”吗?它既可以塞进圆形孔中,也可以塞进方形孔中,还可以塞进三角形孔中,如图所示,请你画出它的三视图,并说说你从中得到的启发.你能用类似的方法设计其他多用塞子吗?
我们见过的瓶塞大都是圆柱形的.你见过一种“三用瓶塞”吗?它既可以塞进圆形孔中,也可以塞进方形孔中,还可以塞进三角形孔中,如图所示,请你画出它的三视图,并说说你从中得到的启发.你能用类似的方法设计其他多用塞子吗?