题目内容
3.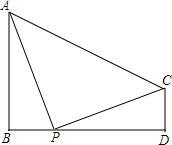 如图,已知AB丄BD,CD丄BD.
如图,已知AB丄BD,CD丄BD.(1)若AB=9,CD=4,BD=10,请问在BD上是否存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?若存在,求BP的长;若不存在.请说明理由;
(2)若AB=9,CD=4,BD=12,请问在BD上存在多少个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为頂点的三角形相似?并求BP的长.
分析 (1)设BP=x,则PD=10-x,由于∠B=∠D,根据两组对应边的比相等且夹角对应相等的两个三角形相似,则当$\frac{AB}{PD}$=$\frac{PB}{DC}$时,△ABP∽△PDC,即$\frac{9}{10-x}$=$\frac{x}{4}$,当$\frac{AB}{CD}$=$\frac{PB}{PD}$时,△ABP∽△CDP,即$\frac{9}{4}$=$\frac{x}{10-x}$,然后分别解方程求出x的值即可得到BP的长;
(2)设BP=x,则PD=12-x,与(1)解答一样,易得$\frac{9}{12-x}$=$\frac{x}{4}$或$\frac{9}{4}$=$\frac{x}{12-x}$,然后分别解方程求出x的值即可得到BP的长.
解答 解:(1)存在.
设BP=x,则PD=10-x,
∵∠B=∠D,
∴当$\frac{AB}{PD}$=$\frac{PB}{DC}$时,△ABP∽△PDC,即$\frac{9}{10-x}$=$\frac{x}{4}$,
整理得x2-10x+36=0,此方程没有实数解;
当$\frac{AB}{CD}$=$\frac{PB}{PD}$时,△ABP∽△CDP,即$\frac{9}{4}$=$\frac{x}{10-x}$,即解得x=$\frac{90}{13}$,
即BP的长为$\frac{19}{13}$;
(2)存在2个P点.
设BP=x,则PD=12-x,
∵∠B=∠D,
∴当$\frac{AB}{PD}$=$\frac{PB}{DC}$时,△ABP∽△PDC,即$\frac{9}{12-x}$=$\frac{x}{4}$,
整理得x2-12x+36=0,解得x1=x2=6;
当$\frac{AB}{CD}$=$\frac{PB}{PD}$时,△ABP∽△CDP,即$\frac{9}{4}$=$\frac{x}{12-x}$,即解得x=$\frac{108}{13}$,
即BP的长为6或$\frac{108}{13}$.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.注意分类讨论思想的运用.

 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案| A. | (5,-4) | B. | (-5,4) | C. | (5,-4)或(-5,4) | D. | (4,-5)或(-4,5) |
 探索规律:观察下面由组成的图案和算式,解答问题:
探索规律:观察下面由组成的图案和算式,解答问题: 如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.求证:PC=CQ.
如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BC相交于点P,BE与CD相交于点Q,连接PQ.求证:PC=CQ.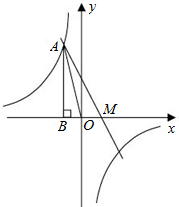 如图,已知反比例函数$y=\frac{k}{x}$的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数$y=\frac{k}{x}$的图象上另一点C(n,-2).
如图,已知反比例函数$y=\frac{k}{x}$的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数$y=\frac{k}{x}$的图象上另一点C(n,-2). 如图,已知∠ACE是ABC的一个外角,DC平分∠ACE,且AB∥CD,求证:△ABC为等腰三角形.
如图,已知∠ACE是ABC的一个外角,DC平分∠ACE,且AB∥CD,求证:△ABC为等腰三角形.