题目内容
16.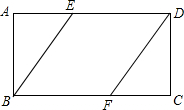 如图,在矩形ABCD中,AB=4,BC=8,点E、F分别在AD和BC上,若AE=CF.(1)求证:四边形DEBF是平行四边形;
如图,在矩形ABCD中,AB=4,BC=8,点E、F分别在AD和BC上,若AE=CF.(1)求证:四边形DEBF是平行四边形;(2)当AE的长是多少时,四边形BEDF是菱形?
分析 (1)根据一组对边平行且相等判断四边形DEBF是平行四边形即可;
(2)根据有一组邻边相等的平行四边形是菱形即可求出AE的值.
解答  (1)证明:∵四边形ABCD是矩形,
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∴ED∥BF.
又AE=CF,
∴ED=BF,
∴四边形DEBF是平行四边形.
(2)解:设AE=x,则DE=BE=8-x,
在Rt△ABE中,AB2+AE2=BE2,42+x2=(8-x)2,
解得:AE=x=3,
∴当AE=3时,四边形DEBF是菱形.
点评 本题考查平行四边形和菱形的判定,难度适中,解题关键是熟练掌握它们的判定方法并灵活运用.

练习册系列答案
相关题目
5.下列结论正确的是( )
| A. | 平行四边形是轴对称图形 | B. | 菱形的对角线互相垂直且相等 | ||
| C. | 正方形的对称轴有4条 | D. | 矩形的对角线互相垂直 |
7.下列计算正确的是( )
| A. | (a-$\frac{1}{2}$b)2=a2-$\frac{1}{2}$ab+$\frac{1}{4}$b2 | B. | -2a2($\frac{1}{2}$ab+b2)=-a3b+b2a2 | ||
| C. | -$\frac{1}{2}$a2bn•(3anbn+1)=-$\frac{3}{2}$a2nb${\;}^{{n}^{2}+n}$ | D. | (a-b)(-a-2b)=-a2-ab+2b2 |
11.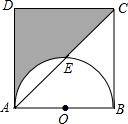 如图所示,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E,则图中阴影部分的面积为( )
如图所示,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E,则图中阴影部分的面积为( )
 如图所示,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E,则图中阴影部分的面积为( )
如图所示,在边长为4的正方形ABCD中,以AB为直径的半圆与对角线AC交于点E,则图中阴影部分的面积为( )| A. | 10-π | B. | 8-π | C. | 12-π | D. | 6-π |
6.下列的平面几何图形中,既是轴对称图形又是中心对称图形的是( )


| A. | 圆弧 | B. | 角 | C. | 扇形 | D. | 菱形 |
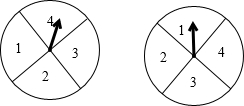 让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则这两个数的和概率最大的和等于( )
让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则这两个数的和概率最大的和等于( )