题目内容
2.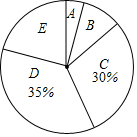 今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:(1)求全班学生人数和m、n的值;
(2)求扇形统计图中“B”区对应的圆心角度数;
(3)如果该校九年级共有960人,那么估计分数在56≤x<61的有多少人?
| 分组 | 分数段(分) | 频数 |
| A | 36≤x<41 | 3 |
| B | 41≤x<46 | n |
| C | 46≤x<51 | 18 |
| D | 51≤x<56 | m |
| E | 56≤x<61 | 17 |
分析 (1)根据C组的频数和百分数,即可得到全班学生人数,根据D组的百分比即可得到m的值,进而得到B组的人数;
(2)根据B组的人数占总人数的百分比乘上360°,即可得到扇形统计图中“B”区对应的圆心角度数;
(3)根据分数在56≤x<61的人数所占的比例乘上该校九年级总人数,即可得到分数在56≤x<61的人数.
解答 解:(1)全班学生人数=18÷30%=60,
m=60×35%=21,
n=60-3-18-21-17=1;
(2)扇形统计图中“B”区对应的圆心角度数=$\frac{1}{60}$×360°=6°;
(3)分数在56≤x<61的人数为:$\frac{17}{60}$×960=272(人).
点评 本题主要考查了扇形统计图的应用,解题时注意:通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系,用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
13.下列计算正确的是( )
| A. | a4+a5=a9 | B. | a3•a3•a3=3x3 | C. | (-a3)4=a7 | D. | 2a4•3a5=6a9 |
14.如果(a3)2=64,则a等于( )
| A. | 2 | B. | -2 | C. | ±2 | D. | 以上都不对 |
 如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.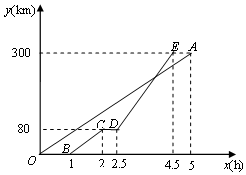 甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:
甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题: 如图所示,菱形ABCD中,对角线相交于点O,E为AD边中点,菱形ABCD 周长为16,则OE的长为( )
如图所示,菱形ABCD中,对角线相交于点O,E为AD边中点,菱形ABCD 周长为16,则OE的长为( ) 如图,菱形ABCD中,过A作BD的平行线交CD的延长线于点E,下列结论:(1)∠EAC=90°,(2)DA=DE,(3)∠ABC=2∠E,其中正确的有( )
如图,菱形ABCD中,过A作BD的平行线交CD的延长线于点E,下列结论:(1)∠EAC=90°,(2)DA=DE,(3)∠ABC=2∠E,其中正确的有( )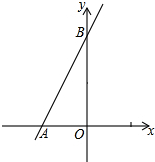 如图,直线y=2x+2与x轴相交于点A,与y轴相交于点B.
如图,直线y=2x+2与x轴相交于点A,与y轴相交于点B.