题目内容
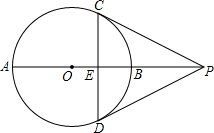 如图,在⊙O中,点P在直径AB的延长线上,PC,PD与⊙O相切,切点分别为点C,点D,连接CD交AB于点E.如果⊙O的半径等于3
如图,在⊙O中,点P在直径AB的延长线上,PC,PD与⊙O相切,切点分别为点C,点D,连接CD交AB于点E.如果⊙O的半径等于3| 5 |
| 1 |
| 2 |
考点:切线的性质
专题:
分析:根据切线的性质得出OC⊥PC,PC=PD,∠OPC=∠OPD,CD⊥OP,CD=2CE.根据tan∠CPO=
,得出tan∠OCE=tan∠CPO=
,设OE=k,则CE=2k,OC=
k.根据已知得出
k=3
,解得k=3.从而得出CE=6.就可求得CD=12.
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
| 5 |
解答: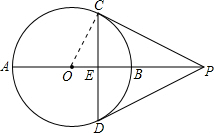 解:连接OC.
解:连接OC.
∵PC,PD与⊙O相切,切点分别为点C,点D,
∴OC⊥PC,PC=PD,∠OPC=∠OPD.CD⊥OP,CD=2CE.
∵tan∠CPO=
,
∴tan∠OCE=tan∠CPO=
,
∴设OE=k,则CE=2k,OC=
k.
∵⊙O的半径等于3
,
∴
k=3
,解得k=3.
∴CE=6.
∴CD=2CE=12.
 解:连接OC.
解:连接OC.∵PC,PD与⊙O相切,切点分别为点C,点D,
∴OC⊥PC,PC=PD,∠OPC=∠OPD.CD⊥OP,CD=2CE.
∵tan∠CPO=
| 1 |
| 2 |
∴tan∠OCE=tan∠CPO=
| 1 |
| 2 |
∴设OE=k,则CE=2k,OC=
| 5 |
∵⊙O的半径等于3
| 5 |
∴
| 5 |
| 5 |
∴CE=6.
∴CD=2CE=12.
点评:本题考查了切线的性质同角的余角相等,解直角三角形等,熟练掌握切线的性质,以及作出辅助线构建直角三角形是关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
 如图,直线a∥b.直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠1=32°,则∠2=
如图,直线a∥b.直线c与直线a,b分别相交于点A、点B,AM⊥b,垂足为点M,若∠1=32°,则∠2= 如图,已知正方形ABCD的边长为4,点E、F分别在边AB,BC上,且AE=BF=1,则OC=
如图,已知正方形ABCD的边长为4,点E、F分别在边AB,BC上,且AE=BF=1,则OC=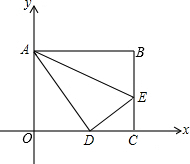 如图,平面直角坐标系中,矩形OABC的顶点B(10,8),点A在y轴上,点C在x轴上,E为BC上一点,把△ABE沿ZE折叠,点B落在OC上的D处.
如图,平面直角坐标系中,矩形OABC的顶点B(10,8),点A在y轴上,点C在x轴上,E为BC上一点,把△ABE沿ZE折叠,点B落在OC上的D处. 如图是时代超市某种牛奶的价格标签,请在横线上写出它的原价.
如图是时代超市某种牛奶的价格标签,请在横线上写出它的原价.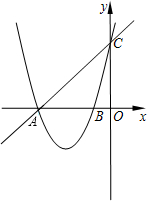 如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+kx+k-1图象过点A和点C,抛物线与x轴的另一交点是B,
如图,在平面直角坐标系内,已知直线y=x+4与x轴、y轴分别相交于点A和点C,抛物线y=x2+kx+k-1图象过点A和点C,抛物线与x轴的另一交点是B,