题目内容
 如图,已知正方形ABCD的边长为4,点E、F分别在边AB,BC上,且AE=BF=1,则OC=
如图,已知正方形ABCD的边长为4,点E、F分别在边AB,BC上,且AE=BF=1,则OC=考点:全等三角形的判定与性质,正方形的性质,相似三角形的判定与性质
专题:
分析:首先证明△BEC≌△CFD,即可证明OC⊥DF,然后利用直角三角新的面积公式即可求得OC的长.
解答:解:∵正方形ABCD中,AB=BC=CD=4,∠B=∠DCF,
又∵AE=BF,
∴BE=CF=4-1=3,DF=
=
=5,
则在直角△BEC和直角△CFD中,
,
∴△BEC≌△CFD,
∴∠BEC=∠CFD,
又∵直角△BCE中,∠BEC+∠BCE=90°,
∴∠CFD+∠BCE=90°,
∴∠FOC=90°,即OC⊥DF,
∴S△CDF=
CD•CF=
OC•DF,
∴OC=
=
=
.
故答案是:
.
又∵AE=BF,
∴BE=CF=4-1=3,DF=
| CD2+CF2 |
| 42+32 |
则在直角△BEC和直角△CFD中,
|

∴△BEC≌△CFD,
∴∠BEC=∠CFD,
又∵直角△BCE中,∠BEC+∠BCE=90°,
∴∠CFD+∠BCE=90°,
∴∠FOC=90°,即OC⊥DF,
∴S△CDF=
| 1 |
| 2 |
| 1 |
| 2 |
∴OC=
| CF•CD |
| DF |
| 3×4 |
| 5 |
| 12 |
| 5 |
故答案是:
| 12 |
| 5 |
点评:本题考查了正方形的性质,以及全等三角形的判定与性质,证明△BEC≌△CFD是解题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
单项式22pm2n2的次数是( )
| A、4 | B、5 | C、6 | D、7 |
抛物线y=x2-mx-m2+1的图象过原点,则m为( )
| A、0 | B、1 | C、-1 | D、±1 |
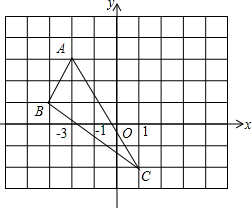 如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).
如图,△ABC的三个顶点的坐标分别是A(-2,3),B(-3,1),C(1,-2).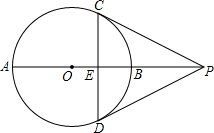 如图,在⊙O中,点P在直径AB的延长线上,PC,PD与⊙O相切,切点分别为点C,点D,连接CD交AB于点E.如果⊙O的半径等于3
如图,在⊙O中,点P在直径AB的延长线上,PC,PD与⊙O相切,切点分别为点C,点D,连接CD交AB于点E.如果⊙O的半径等于3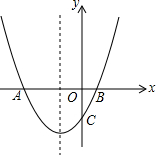 如图,抛物线y=
如图,抛物线y=