题目内容
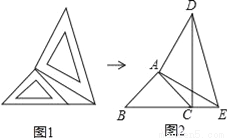
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)求证:△ABE≌△ACD;
(2)求证:DC⊥BE.
练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
题目内容
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
(1)求证:△ABE≌△ACD;
(2)求证:DC⊥BE.

 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案