题目内容
2. 如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=$\sqrt{3}$,求ED的长.
分析 (1)由Rt△BAE≌Rt△CDF,推出∠1=∠F,推出BE∥CF,又BE=CF,即可证明四边形EBCF是平行四边形;
(2)Rt△BAE中,∠2=30°,AB=$\sqrt{3}$,求出AE、BE,在Rt△BEC中,求出BC,由此即可解决问题.
解答 (1)证明: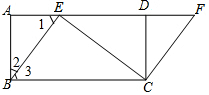
∵四边形ABCD是矩形,
∴∠A=∠CDF=∠ABC=90°,AB=DC,AD=BC,
在Rt△BAE和Rt△CDF中,
$\left\{\begin{array}{l}AB=DC\\ BE=CF\end{array}\right.$,
∴Rt△BAE≌Rt△CDF,
∴∠1=∠F,
∴BE∥CF,
又∵BE=CF,
∴四边形EBCF是平行四边形.
(2)解:∵Rt△BAE中,∠2=30°,AB=$\sqrt{3}$,
∴AE=AB•tan∠2=1,$BE=\frac{AB}{cos∠2}=2$,∠3=60°,
在Rt△BEC中,$BC=\frac{BE}{cos∠3}=\frac{2}{cos60°}=4$,
∴AD=BC=4,
∴ED=AD-AE=4-1=3.
点评 本题考查矩形的性质、平行四边形的判定.解直角三角形,锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
7. 如图,OA为⊙O的半径,弦BC⊥OA于P点.若OA=5,AP=2,则弦BC的长为( )
如图,OA为⊙O的半径,弦BC⊥OA于P点.若OA=5,AP=2,则弦BC的长为( )
 如图,OA为⊙O的半径,弦BC⊥OA于P点.若OA=5,AP=2,则弦BC的长为( )
如图,OA为⊙O的半径,弦BC⊥OA于P点.若OA=5,AP=2,则弦BC的长为( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
 如图,在等边△ABC中,边长为30,点M为线段AB上一动点,将等边△ABC沿过M的直线折叠,折痕与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,设折痕为MN,则AN的值为21或65.
如图,在等边△ABC中,边长为30,点M为线段AB上一动点,将等边△ABC沿过M的直线折叠,折痕与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,设折痕为MN,则AN的值为21或65.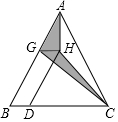 如图,△ABC的面积为16,点D是BC边上一点,且BD=$\frac{1}{4}$BC,点G是AB上一点,点B在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是4.
如图,△ABC的面积为16,点D是BC边上一点,且BD=$\frac{1}{4}$BC,点G是AB上一点,点B在△ABC内部,且四边形BDHG是平行四边形,则图中阴影部分的面积是4. 如图,矩形ABCD的对角线BD的中点为O,过点O作OE⊥BC于点E,连接OA,已知AB=5,BC=12,则四边形ABEO的周长为20.
如图,矩形ABCD的对角线BD的中点为O,过点O作OE⊥BC于点E,连接OA,已知AB=5,BC=12,则四边形ABEO的周长为20. 如图,在?ABCD中,∠A=45°,AB=2,AD=4,将?ABCD折叠,使D,C的对应点E,F都落在直线AB上,折痕为MN,则AF=2+2$\sqrt{2}$.
如图,在?ABCD中,∠A=45°,AB=2,AD=4,将?ABCD折叠,使D,C的对应点E,F都落在直线AB上,折痕为MN,则AF=2+2$\sqrt{2}$.