题目内容
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2.
其中正确的有( )

A.①②③ B.②④ C.②⑤ D.②③⑤
D【考点】二次函数图象与系数的关系.
【专题】数形结合.
【分析】根据抛物线开口方向得a<0,由抛物线对称轴为直线x=﹣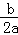 =1,得到b=
=1,得到b= ﹣2a>0,即2a+b=0,由抛物线与y轴的交点位置得到c>0,所以abc<0;根据二次函数的性质得当x=1时,函数有最大值a+b+c,则当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm;根据抛物线的对称性得到抛物线与x轴的另一个交点在(﹣1,0)的右侧,则当x=﹣1时,y<0,所以a﹣b+c<0;把ax12+bx1=ax22+bx2先移项,再分解因式得到(x1﹣x2)[a(x1+x2)+b]=0,而x1≠x2,则a(x1+x2)+b=0,即x1+x2=﹣
﹣2a>0,即2a+b=0,由抛物线与y轴的交点位置得到c>0,所以abc<0;根据二次函数的性质得当x=1时,函数有最大值a+b+c,则当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm;根据抛物线的对称性得到抛物线与x轴的另一个交点在(﹣1,0)的右侧,则当x=﹣1时,y<0,所以a﹣b+c<0;把ax12+bx1=ax22+bx2先移项,再分解因式得到(x1﹣x2)[a(x1+x2)+b]=0,而x1≠x2,则a(x1+x2)+b=0,即x1+x2=﹣ ,然后把b=﹣2a代入计算得到x1+x2=2.
,然后把b=﹣2a代入计算得到x1+x2=2.
【解答】解:∵抛物线开口向下,
∴a<0,
∵抛物线对称轴为直线x=﹣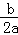 =1,
=1,
∴b=﹣2a>0,即2a+b=0,所以②正确;
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵抛物线对称轴为直线x=1,
∴函数的最大值为a+b+c,
∴当m≠1时,a+b+c>am2+bm+c,即a+b>am2+bm,所以③正确;
∵抛物线与x轴的一个交点在(3,0)的左侧,而对称轴为直线x=1,
∴抛物线与x轴的另一个交点在(﹣1,0)的右侧
∴当x=﹣1时,y<0,
∴a﹣b+c<0,所以④错误;
∵ax12+bx1=ax22+bx2,
∴ax12+bx1﹣ax22﹣bx2=0,
∴a(x1+x2)(x1﹣x2)+b(x1﹣x2)=0,
∴(x1﹣x2)[a(x1+x2)+b]=0,
而x1≠x2,
∴a(x1+x2)+b=0,即x1+x2=﹣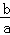 ,
,
∵b=﹣2a,
∴x1+x2=2,所以⑤正确.
故选:D.
【点评】本题考查了二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线开口向上;当a<0时,抛物线开口向下;一次项系数b和 二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左侧;当a与b异号时(即ab<0),对称轴在y轴右侧;常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.
二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左侧;当a与b异号时(即ab<0),对称轴在y轴右侧;常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.

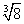 是无理数; D.点(-2,-3)关于
是无理数; D.点(-2,-3)关于 轴对称的点是(-2,3);
轴对称的点是(-2,3); 的正整数解是 .
的正整数解是 . B和点C分别以每秒3个
B和点C分别以每秒3个
 =__________.
=__________.