题目内容
Rt△ABC中,∠A=90°,AB=2,AC=4,点E、F分别为AB和AC上的点,且△AEF和△ABC相似,作AD⊥EF于点D,当AE=1时,AD的长为 .
考点:相似三角形的判定与性质
专题:
分析:因为两个相似三角形的对应边不确定,所以需要分类讨论;借助相似三角形的性质及勾股定理,运用三角形的面积公式即可解决问题.
解答:解:若△AEF∽△ABC,则
=
;
当AE=1时,AF=
=
=2,
此时EF=
=
,由三角形的面积公式得:
EF•AD=
AE•AF,
∴AD=
=
=
;
若△AEF∽△ACB,则
=
,
当AE=1时,AF=
=
=
,此时EF=
=
=
;
由三角形的面积公式得:
EF•AD=
AE•AF,
∴AD=
=
=
;
综上所述,AD的长为
或
;
该题答案为
或
| AE |
| AB |
| AF |
| AC |
当AE=1时,AF=
| AE•AC |
| AB |
| 1×4 |
| 2 |
此时EF=
| 12+22 |
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
| AE•AF |
| EF |
| 1×2 | ||
|
2
| ||
| 5 |
若△AEF∽△ACB,则
| AE |
| AC |
| AF |
| AB |
当AE=1时,AF=
| AE•AB |
| AC |
| 1×2 |
| 4 |
| 1 |
| 2 |
12+(
|
|
| ||
| 2 |
由三角形的面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
| AE•AF |
| EF |
1×
| ||||
|
| ||
| 5 |
综上所述,AD的长为
2
| ||
| 5 |
| ||
| 5 |
该题答案为
2
| ||
| 5 |
| ||
| 5 |
点评:该题主要考查了相似三角形的性质及其应用问题;解题的关键是借助分类讨论的数学思想,按两种情况分类解决;对分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
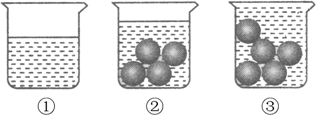
如图是测量一颗玻璃球体积的过程:
(1)将300mL的水倒进一个容量为500mL的杯子中;
(2)将四颗相同的玻璃球放入水中,结果水没有满;(3)再加一颗同样的玻璃球放入水中,结果水满溢出.
根据以上过程,推测这样一颗玻璃球的体积在(1mL水的体积为1cm3)( )
(1)将300mL的水倒进一个容量为500mL的杯子中;
(2)将四颗相同的玻璃球放入水中,结果水没有满;(3)再加一颗同样的玻璃球放入水中,结果水满溢出.
根据以上过程,推测这样一颗玻璃球的体积在(1mL水的体积为1cm3)( )

| A、20cm3以上,30cm3以下 |
| B、30cm3以上,40cm3以下 |
| C、40cm3以上,50cm3以下 |
| D、50cm3以上,60cm3以下 |
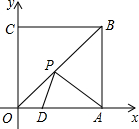 如图所示,四边形OABC为正方形,点A,C分别在x轴,y轴的正半轴上,点D在OA上,在OB上求作一点P,使得PD+PA的值最小,则可连接( )
如图所示,四边形OABC为正方形,点A,C分别在x轴,y轴的正半轴上,点D在OA上,在OB上求作一点P,使得PD+PA的值最小,则可连接( )| A、AC | B、BD | C、CD | D、不确定 |
小敏同学利用计算机设计了一个计算程序,输入和输出的数据如下表:当输入数据是20时,输出的数据是
( )
( )
| 输入 | 1 | 2 | 3 | 4 | 5 | … | ||||||||||
| 输出 |
|
|
|
|
| … |
A、
| ||
B、
| ||
C、
| ||
D、
|
 我们给出如下定义:点P是等边△ABC内一点,连结PA,PB,PC,我们称以PA,PB,PC为边构成的新三角形为原三角形的“联谊三角形”.
我们给出如下定义:点P是等边△ABC内一点,连结PA,PB,PC,我们称以PA,PB,PC为边构成的新三角形为原三角形的“联谊三角形”.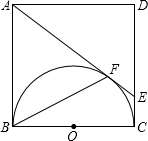 如图,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A点作半圆的切线,与半圆相切于点F,与DC相交于点E,求BF的长.
如图,正方形ABCD的边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A点作半圆的切线,与半圆相切于点F,与DC相交于点E,求BF的长.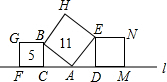 如图,直线l上方有三个正方形,若两个面积分别为5和11,则正方形DMNE的面积等于
如图,直线l上方有三个正方形,若两个面积分别为5和11,则正方形DMNE的面积等于