题目内容
已知点A(-1,-2)和点B(4,2),若点C的坐标为(1,m),当m为多少时,AC+AB有最小值?
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:连接AB,交直线x=1于C,此时AC+AB有最小值;利用待定系数法求得直线AB的解析式,把x=1代入即可求得m的值.
解答: 解:连接AB,交直线x=1于C,此时AC+AB有最小值;
解:连接AB,交直线x=1于C,此时AC+AB有最小值;
设直线AB的解析式为y=kx+b,
∴
,解得
,
∴直线AB的解析式为y=
x-
,
把x=1代入,得y=
×1-
=-
,
∴C的坐标为(1,-
),
∴当m=-
时,AC+AB有最小值.
 解:连接AB,交直线x=1于C,此时AC+AB有最小值;
解:连接AB,交直线x=1于C,此时AC+AB有最小值;设直线AB的解析式为y=kx+b,
∴
|
|
∴直线AB的解析式为y=
| 4 |
| 5 |
| 6 |
| 5 |
把x=1代入,得y=
| 4 |
| 5 |
| 6 |
| 5 |
| 2 |
| 5 |
∴C的坐标为(1,-
| 2 |
| 5 |
∴当m=-
| 2 |
| 5 |
点评:本题考查了最短路线问题,待定系数法的应用,坐标和图形的性质等,找出C点是本题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
已知实数a、b、c满足a<0,4a-2b+c>0,则一定有( )
| A、b2-4ac>0 |
| B、b2-4ac<0 |
| C、b2-4ac≥0 |
| D、b2-4ac≤0 |
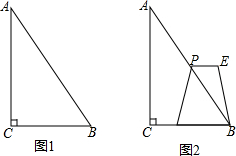 如图,△ABC中,∠C=Rt∠,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒.
如图,△ABC中,∠C=Rt∠,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒.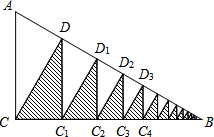 如图,已知Rt△ABC中,∠B=30°,AC=2,作△CDB的高DC1,作△DC1B的高C1D1,…,就这样无限作下去,求图中阴影部分的面积.
如图,已知Rt△ABC中,∠B=30°,AC=2,作△CDB的高DC1,作△DC1B的高C1D1,…,就这样无限作下去,求图中阴影部分的面积.