题目内容
若P=x-y,Q=y-z,且P+Q+R=0,则R= .
考点:整式的加减
专题:
分析:先由P+Q+R=0,得出R=-P-Q,再将P=x-y,Q=y-z代入,去括号合并同类项即可.
解答:解:∵P+Q+R=0,
∴R=-P-Q,
∵P=x-y,Q=y-z,
∴R=-(x-y)-(y-z)
=-x+y-y+z
=-x+z.
故答案为-x+z.
∴R=-P-Q,
∵P=x-y,Q=y-z,
∴R=-(x-y)-(y-z)
=-x+y-y+z
=-x+z.
故答案为-x+z.
点评:本题考查了整式的加减、去括号法则两个考点.解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.

练习册系列答案
相关题目
 如图,等腰△ABC的底边BC=10cm,顶角为120°,求它的外接圆的直径.
如图,等腰△ABC的底边BC=10cm,顶角为120°,求它的外接圆的直径. 如图,已知,AB=AC,F是BC上的一点,且FE⊥AC于E,FG⊥AB于G,CD⊥AB于D,求证:FG+FE=CD.
如图,已知,AB=AC,F是BC上的一点,且FE⊥AC于E,FG⊥AB于G,CD⊥AB于D,求证:FG+FE=CD.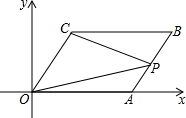 如图,平行四边形OABC在平面直角坐标系中,A(4,0)、C(1,3).
如图,平行四边形OABC在平面直角坐标系中,A(4,0)、C(1,3).