题目内容
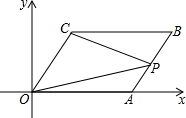 如图,平行四边形OABC在平面直角坐标系中,A(4,0)、C(1,3).
如图,平行四边形OABC在平面直角坐标系中,A(4,0)、C(1,3).(1)求B点的坐标;
(2)若P是线段AB上的动点,问
| ∠PCB+∠POA |
| ∠CPO |
(3)若P是线段AB上的动点,
| S △BCP+S △OAP |
| S 四边形OABC |
考点:平行四边形的性质,坐标与图形性质
专题:
分析:(1)由条件可知B点的纵坐标和C点的相同,延长BC交y轴于点D,可求得BD的长,可求得B点的横坐标;
(2)过点P作PE∥BC,交OC于点E,则由平行的性质可得出∠PCB+∠POA=∠CPO,可得出结论;、
(3)设平行四边形OABC的AB边上的高为h,则可表示出△BCP和△OAP的面积和,表示出平行四边形OABC的面积,可找出其关系,得出结论.
(2)过点P作PE∥BC,交OC于点E,则由平行的性质可得出∠PCB+∠POA=∠CPO,可得出结论;、
(3)设平行四边形OABC的AB边上的高为h,则可表示出△BCP和△OAP的面积和,表示出平行四边形OABC的面积,可找出其关系,得出结论.
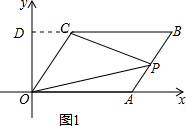
解答:解:(1)如图1,延长BC交y轴于点D,
∵四边形OABC为平行四边形,
∴BC=OA=4,且C点坐标为(1,3),
∴CD=1,OD=3,
∴B点坐标为(5,3);
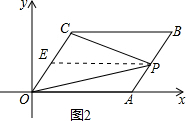
(2)如图2,过点P作PE∥BC,交OC于点E,
∵BC∥OA,
∴PE∥OA,
∴∠BCP=∠CPE,∠POA=∠OPE,
∴∠OPC=∠CPE+OPE=∠BCP+∠POA,
∴
=
=1,
∴
是定值,其值为1;
(3)设平行四边形OABC的AB边上的高为h,
则S△BCP=
BP•h,S△OAP=
AP•h,S平行四边形OABC=AB•h,
所以S△BCP+S△OAP=
(BP+AP)h=
AB•h=
S平行四边形OABC,
所以
=
=
,
所以
是定值,其值为
.
∵四边形OABC为平行四边形,
∴BC=OA=4,且C点坐标为(1,3),
∴CD=1,OD=3,
∴B点坐标为(5,3);

(2)如图2,过点P作PE∥BC,交OC于点E,
∵BC∥OA,
∴PE∥OA,
∴∠BCP=∠CPE,∠POA=∠OPE,
∴∠OPC=∠CPE+OPE=∠BCP+∠POA,
∴
| ∠PCB+∠POA |
| ∠CPO |
| ∠CPO |
| ∠CPO |
∴
| ∠PCB+∠POA |
| ∠CPO |

(3)设平行四边形OABC的AB边上的高为h,
则S△BCP=
| 1 |
| 2 |
| 1 |
| 2 |
所以S△BCP+S△OAP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以
| S△BCP+S△OAP |
| S四边形OABC |
| ||
| S四边形OABC |
| 1 |
| 2 |
所以
| S △BCP+S △OAP |
| S 四边形OABC |
| 1 |
| 2 |
点评:本题主要考查平行四边形的性质,在(2)(3)中找到角或面积之间的关系是解题的关键.

练习册系列答案
相关题目
 如图,△ABC中,AB=AC,AD∥CB,求证:AD平分∠CAE.
如图,△ABC中,AB=AC,AD∥CB,求证:AD平分∠CAE.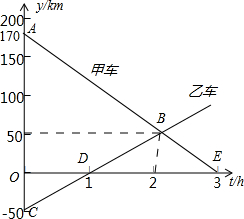 甲、乙两辆汽车在同一条公路上同时匀速行驶,图中的两条线分别表示甲、乙两车距M站的距离y(km)与它们行驶的时间t(h)之间的函数关系式,请根据图象回答下列问题.
甲、乙两辆汽车在同一条公路上同时匀速行驶,图中的两条线分别表示甲、乙两车距M站的距离y(km)与它们行驶的时间t(h)之间的函数关系式,请根据图象回答下列问题.