题目内容
7. 如图,点E、F、G、H分别位于边长为2cm正方形ABCD的四条边上,且四边形EFGH也是正方形.问:当点E位于何处时,正方形EFGH的面积S(cm2)最小?最小面积是多少?
如图,点E、F、G、H分别位于边长为2cm正方形ABCD的四条边上,且四边形EFGH也是正方形.问:当点E位于何处时,正方形EFGH的面积S(cm2)最小?最小面积是多少?
分析 因为正方形ABCD的边长为2cm,设AE=x,则BE=2-x,易证△AHE≌△BEF≌△CFG≌△DHG,再利用勾股定理求出EF的长,进而得到正方形EFGH的面积,利用二次函数的性质即可求出面积的最小值.
解答 解:∵正方形ABCD的边长为2cm,设AE=x,
∴BE=2-x,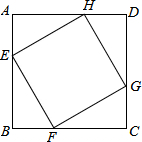
∵四边形EFGH是正方形,
∴EH=EF,∠HEF=90°,
∴∠AEH+∠BEF=90°,
∵∠AEH+∠AHE=90°,
∴∠AHE=∠BEF,
在△AHE和△BEF中,
$\left\{\begin{array}{l}{∠A=∠B=90°}\\{∠AHE=∠BEF}\\{EH=EF}\end{array}\right.$,
∴△AHE≌△BEF(AAS),
同理可证△AHE≌△BEF≌△CFG≌△DHG,
∴AE=BF=CG=DH=x,AH=BE=CF=DG=2-x,
∴EF2=BE2+BF2=(2-x)2+x2=2x2-4x+42,
∴正方形EFGH的面积S=EF2=2x2-4x+42=2(x-1)2+2,
即:当x=1(即E在AB边上的中点)时,正方形EFGH的面积最小,最小的面积为2.
点评 本题考查了正方形的性质、全等三角形的判定和性质以及二次函数的性质,题目的综合性较强,难度中等.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
2.下列结论正确的是( )
| A. | 若a>b,则a2>b2 | B. | 若a2>b2,则a>b | C. | 若a>b,则a3>b3 | D. | 若a3>b3,则a2>b2 |
12.一元二次方程(x-2)=x(x-2)的解是( )
| A. | x=1 | B. | x=2 | C. | x1=2,x2=0 | D. | x1=1,x2=2 |