题目内容
2.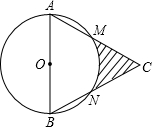 如图,等边△ABC边长为12cm,以AB为直径的⊙O分别交CA、CB于M、N两点,则图中阴影部分的面积是( )
如图,等边△ABC边长为12cm,以AB为直径的⊙O分别交CA、CB于M、N两点,则图中阴影部分的面积是( )| A. | 9$\sqrt{3}$-6π | B. | 18$\sqrt{3}$-6π | C. | 12$\sqrt{3}$-3π | D. | 12$\sqrt{3}$-6π |
分析 连接OM,ON,阴影部分面积等于三角形ABC面积减去三角形AOM面积减去三角形BON面积,再减去扇形MON面积,求出即可.
解答  解:连接OM,ON,如图所示:
解:连接OM,ON,如图所示:
∵△ABC为等边三角形,
∴∠A=∠C=60°,AB=AC=BC,
∵OM=ON=OA=OB,
∴△AOM与△BON都为边长为6cm等边三角形,
∴∠MON=60°,
则S阴影=S△ABC-S△AOM-S△BON=$\frac{\sqrt{3}}{4}$×122-2×$\frac{\sqrt{3}}{4}$×62-$\frac{60π×{6}^{2}}{360}$=18$\sqrt{3}$-6π(cm2),
故选B.
点评 此题考查了扇形面积的计算,以及等边三角形的性质,熟练掌握扇形的面积公式是解本题的关键.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
20.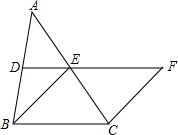 如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
(1)求证:四边形BCFE是菱形;
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.
 如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF(1)求证:四边形BCFE是菱形;
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.
1. 如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
 如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
如图,?ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )| A. | BE=DF | B. | BF=DE | C. | AE=CF | D. | ∠1=∠2 |
14.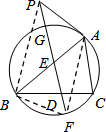 如图,△ABC内接于⊙O,过BC的中点D作直线l∥AC,l与AB交于点E,与⊙O交于点G、F,与⊙O在点A处的切线交于点P,若PE=3,ED=2,EF=3,则PA的长度为( )
如图,△ABC内接于⊙O,过BC的中点D作直线l∥AC,l与AB交于点E,与⊙O交于点G、F,与⊙O在点A处的切线交于点P,若PE=3,ED=2,EF=3,则PA的长度为( )
 如图,△ABC内接于⊙O,过BC的中点D作直线l∥AC,l与AB交于点E,与⊙O交于点G、F,与⊙O在点A处的切线交于点P,若PE=3,ED=2,EF=3,则PA的长度为( )
如图,△ABC内接于⊙O,过BC的中点D作直线l∥AC,l与AB交于点E,与⊙O交于点G、F,与⊙O在点A处的切线交于点P,若PE=3,ED=2,EF=3,则PA的长度为( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
12.下列调查中,适宜采用普查方式的是( )
| A. | 调查市场上酸奶的质量情况 | |
| B. | 调查乘坐飞机的旅客是否携带了危禁物品 | |
| C. | 调查某品牌日光灯管的使用寿命 | |
| D. | 调查《阿福聊斋》节目的收视率情况 |
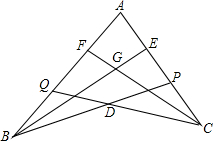 如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,求∠A的度数.
如图,点P在AC上,点Q在AB上,BE平分∠ABP,交AC于E,CF平分∠ACQ,交AB于F,BE、CF相交于G,CQ、BP相交于D,若∠BDC=140°,∠BGC=110°,求∠A的度数.