题目内容
20.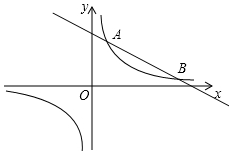 如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A、B两点,点A的坐标为(2,6),点B的坐标为(n,1).
如图,反比例函数y=$\frac{m}{x}$的图象与一次函数y=kx+b的图象交于A、B两点,点A的坐标为(2,6),点B的坐标为(n,1).(1)求反比例函数与一次函数的表达式.
(2)连结OA、OB,求△AOB的面积.
分析 (1)首先利用待定系数法求得反比例函数的解析式,然后把B的坐标代入求得n的值,再利用待定系数法求得一次函数的解析式;
(2)设一次函数y=-$\frac{1}{2}$x+7的图象与x轴相交于C点,根据S△AOB=S△AOC-S△BOC求解.
解答 解:(1)把点A(2,6)的坐标代入y=$\frac{m}{x}$得m=12.∴反比例函数表达式为y=$\frac{12}{x}$.
把点B(n,1)的坐标代入y=$\frac{12}{x}$得n=12.∴B点坐标为(12,1).
设一次函数的表达式为y=kx+b,把A(2,6)、B(12,1)两点坐标代入解得k=-$\frac{1}{2}$,b=7.
∴一次函数的表达式为y=-$\frac{1}{2}$x+7.
(2)设一次函数y=-$\frac{1}{2}$x+7的图象与x轴相交于C点.
则C点坐标为(14,0).
∴OC=14.
∵A点坐标为(2,6),
∴A点到x轴的距离为6.即△AOC的高为6
∴△AOC的面积为:$\frac{1}{2}$×14×6=42.
∵B点坐标为(12,1),∴B点到x轴的距离为1.即△BOC的高为6.
∴△BOC的面积为:$\frac{1}{2}$×14×1=7.
∵S△AOB=S△AOC-S△BOC,
∴S△AOB=42-7=35.
点评 本题考查了反比例函数与一次函数的交点问题:先由点的坐标求函数解析式,然后解由解析式组成的方程组求出交点的坐标,体现了数形结合的思想.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
14.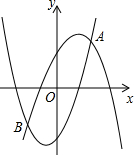 如图,抛物线y1=a(x+1)2-5与抛物线y2=-a(x-1)2+5(a≠0)的交点A,B,点A,B的坐标分别是(2,4),(m,-4),若无论x取何值,y总取y1,y2中的最小值.则y的最大值是( )
如图,抛物线y1=a(x+1)2-5与抛物线y2=-a(x-1)2+5(a≠0)的交点A,B,点A,B的坐标分别是(2,4),(m,-4),若无论x取何值,y总取y1,y2中的最小值.则y的最大值是( )
 如图,抛物线y1=a(x+1)2-5与抛物线y2=-a(x-1)2+5(a≠0)的交点A,B,点A,B的坐标分别是(2,4),(m,-4),若无论x取何值,y总取y1,y2中的最小值.则y的最大值是( )
如图,抛物线y1=a(x+1)2-5与抛物线y2=-a(x-1)2+5(a≠0)的交点A,B,点A,B的坐标分别是(2,4),(m,-4),若无论x取何值,y总取y1,y2中的最小值.则y的最大值是( )| A. | 5 | B. | 4 | C. | 2 | D. | 1 |
8.以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线.如果不考虑空气阻力,球的飞行高度h(米)与飞行时间t(秒)的关系如下表,且h与t的函数关系是我们学过的一次函数、二次函数、反比例函数中的一种
(1)请你从上述函数中选择一种合适的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由
(2)什么时候小球最高?最大高度是多少?
(3)小球运动的时间t在什么范围内,小球在运动过程中的高度不低于18.75米.
| 时间t(秒) | 0 | 1 | 3 | 4 |
| 高度h(米) | 0 | 15 | 15 | 0 |
(2)什么时候小球最高?最大高度是多少?
(3)小球运动的时间t在什么范围内,小球在运动过程中的高度不低于18.75米.
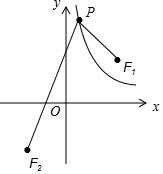 已知直线l1:y=-x+$\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{x}$定点F1($\sqrt{2}$k,$\sqrt{2}$k).
已知直线l1:y=-x+$\sqrt{2}$k,双曲线C:y=$\frac{{k}^{2}}{x}$定点F1($\sqrt{2}$k,$\sqrt{2}$k).