题目内容
9.已知方程ax2+bx+c=0(a≠0)的解是x1=-5,x2=3,那么抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的坐标分别是( )| A. | (0,5),(0,-3) | B. | (-5,0),(3,0) | C. | (0,-5),(0,3) | D. | (5,0),(-3,0) |
分析 求抛物线y=ax2+bx+c(a≠0)与x轴的交点,可令y=0,解方程ax2+bx+c=0(a≠0)得到x1,x2分别是抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的横坐标.
解答 解:抛物线y=ax2+bx+c(a≠0)与x轴相交时,y=0,即ax2+bx+c=0(a≠0),由方程ax2+bx+c=0(a≠0)的解是x1=-5,x2=3可得,抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的坐标分别是(-5,0),(3,0).
故选:B.
点评 本题考查了如何求抛物线与x轴的交点坐标,主要是利用一元二次方程与抛物线的关系来求解.求抛物线y=ax2+bx+c(a≠0)与x轴的交点坐标,令y=0,解方程ax2+bx+c=0(a≠0)即可得到抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的横坐标x1,x2即交点坐标为标(x1,0),(x2,0).

练习册系列答案
相关题目
10.小王第一天做了x个零件,第二天比第一天多做5个,第三天做的零件是第二天的2倍,若三天共做零件75个,则第一天做了( )个.
| A. | 15 | B. | 14 | C. | 10 | D. | 20 |
17.已知二次函数y=a(x+3)2-h(a≠0)有最大值1,则该函数图象的顶点坐标为( )
| A. | (-3,-1) | B. | (-3,1) | C. | (3,1) | D. | (3,-1) |
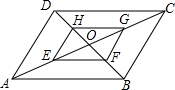 如图,?ABCD的对角线AC、BD相交于点O,点E、F、G、H分别是线段OA、OB、OC、OD的中点,那么?ABCD与四边形EFGH是否是位似图形?为什么?
如图,?ABCD的对角线AC、BD相交于点O,点E、F、G、H分别是线段OA、OB、OC、OD的中点,那么?ABCD与四边形EFGH是否是位似图形?为什么?