题目内容
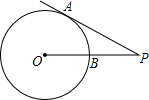
如图，PA切⊙O于A，PB切⊙O于B，OP交⊙O于C，下列结论中，错误的是
- A.∠1=∠2
- B.PA=PB
- C.AB⊥OP
- D.PA2=PC•PO
D
分析：由切线长定理可判断出A、B选项均正确．易知△ABP是等腰三角形，根据等腰三角形三线合一的特点，可求出AB⊥OP，故C正确．而D选项显然不符合切割线定理，因此D错误．
解答：连接OA、OB，AB，
∵PA切⊙O于A，PB切⊙O于B，
由切线长定理知，∠1=∠2，PA=PB，
∴△ABP是等腰三角形，
∵∠1=∠2，
∴AB⊥OP（等腰三角形三线合一），
故A，B，C正确，
根据切割线定理知：PA2=PC•（PO+OC），因此D错误．
故选D．
点评：本题利用了切线长定理，等腰三角形的性质求解．
分析：由切线长定理可判断出A、B选项均正确．易知△ABP是等腰三角形，根据等腰三角形三线合一的特点，可求出AB⊥OP，故C正确．而D选项显然不符合切割线定理，因此D错误．
解答：连接OA、OB，AB，
∵PA切⊙O于A，PB切⊙O于B，
由切线长定理知，∠1=∠2，PA=PB，
∴△ABP是等腰三角形，
∵∠1=∠2，
∴AB⊥OP（等腰三角形三线合一），
故A，B，C正确，
根据切割线定理知：PA2=PC•（PO+OC），因此D错误．
故选D．
点评：本题利用了切线长定理，等腰三角形的性质求解．
练习册系列答案
相关题目
如图，PA切⊙O于点A，PO交⊙O于点B，若PA=6，BP=4，则⊙O的半径为（ ）A、
| ||
B、
| ||
| C、2 | ||
| D、5 |
如图，PA切⊙O于点A，PBC是⊙O的割线，且PB=BC，如果PA=3| 2 |
A、3
| ||
| B、3 | ||
C、
| ||
D、2
|
8、如图，PA切⊙O于点A，PBC是⊙O的割线且过圆心，PA=4，PB=2，则⊙O的半径等于（ ）
如图，PA切⊙O于点A，PB切⊙O于点B，如果∠APB=60°，⊙O半径是3，则劣弧AB的长为（ ）A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
如图：PA切⊙O于A，PB切⊙O于B，OP交⊙O于C，下列结论中错误的是（ ）